题目内容

在平行四边形ABCD中，AC与BD相交于点O，∠ABO+∠ADO=90°，且OB=OA，则四边形ABCD是
 
形．
考点：矩形的判定与性质
专题：
分析：根据三角形内角和证明∠BAD=90°，再根据有一个角是直角的平行四边形是矩形求解．
解答：解：∵∠ABO+∠ADO=90°，
∴∠BAD=180°-90°=90°，
∵四边形ABCD是平行四边形，
∴平行四边形ABCD一定是矩形．
故答案为：矩．
点评：本题考查了矩形的判定与性质，解题的关键是了解矩形的判定定理，难度不大．
练习册系列答案
相关题目
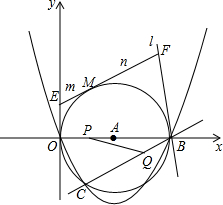如图，在平面直角坐标系中，O为坐标原点，抛物线y=ax2+bx+c（a≠0）过O、B、C三点，B、C坐标分别为（10，0）和（
18
5
，-
24
5
），以OB为直径的⊙A经过C点，直线l垂直x轴于B点．
（1）求直线BC的解析式；
（2）求抛物线解析式及顶点坐标；
（3）点M是⊙A上一动点（不同于O，B），过点M作⊙A的切线，交y轴于点E，交直线l于点F，设线段ME长为m，MF长为n，请猜想m•n的值，并证明你的结论；
（4）若点P从O出发，以每秒一个单位的速度向点B作直线运动，点Q同时从B出发，以相同速度向点C作直线运动，经过t（0＜t≤8）秒时恰好使△BPQ为等腰三角形，请求出满足条件的t值．
计算：
（1）
12
+(
1
2
)-1-|
3
-2|-(π-3)0；       
（2）(
2
-1)2-(
32
-2)÷2
2
．
Rt△ABC中，∠C=90°，点D，E分别是边AC，BC上的点，点P是一动点．令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α．
（1）若点P在线段AB上，如图①，且∠α=50°，则∠1+∠2=
 
；
（2）若点P在斜边AB上运动，如图②，则∠α、∠1、∠2之间的关系为
 
；
（3）如图③，若点P在斜边BA的延长线上运动（CE＜CD），请直接写出∠α、∠1、∠2之间的关系：
 
；
（4）若点P运动到△ABC形外（只需研究图④情形），则∠α、∠1、∠2之间有何关系？并说明理由．
如图①，已知：在矩形ABCD的边AD上有一点O，OA=
3
，以O为圆心，OA长为半径作圆，交AD于M，恰好与BD相切于H，过H作弦HP∥AB，弦HP=3．若点E是CD边上一动点（点E与C，D不重合），过E作直线EF∥BD交BC于F，再把△CEF沿着动直线EF对折，点C的对应点为G．设CE=x，△EFG与矩形ABCD重叠部分的面积为S．
（1）求证：四边形ABHP是菱形；
（2）问△EFG的直角顶点G能落在⊙O上吗？若能，求出此时x的值；若不能，请说明理由；
（3）求S与x之间的函数关系式，并直接写出FG与⊙O相切时，S的值．
计算：
64
-
3-64
+
327
=
 
．
小明解方程组
x+y=△
2x-y=1
，得到解为
x=2
y=●
，由于不小心，滴上了两滴墨水，刚好遮住了两个数△和●，则数△=
 
．
下列调查：
①调查市场上老酸奶的质量情况；
②调查某品牌圆珠笔芯的使用寿命；
③了解炮弹的杀伤半径；
④调查全班同学的身高情况．
其中适宜采用抽样调查的有
 
．
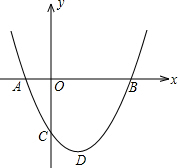如图，二次函数y=ax2+bx+c（a＞0）图象的顶点为D，其图象与x轴的交点A、B的横坐标分别为-1，3．与y轴负半轴交于点C，在下面五个结论中：
①2a-b=0；②a+b+c＞0；③c=-3a；④只有当a=
1
2
时，△ABD是等腰直角三角形；⑤使△ACB为等腰三角形的a值可以有四个．
其中正确的结论是
 
．（只填序号）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网