题目内容
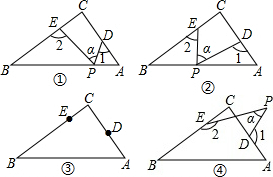
 如图,已知直角梯形ABCD的一条对角线把梯形分为一个直角三角形和一个以BC为底的等腰三角形.若梯形上底为5,则连接△DBC两腰中点的线段的长为
如图,已知直角梯形ABCD的一条对角线把梯形分为一个直角三角形和一个以BC为底的等腰三角形.若梯形上底为5,则连接△DBC两腰中点的线段的长为考点:直角梯形,等腰三角形的性质,三角形中位线定理
专题:几何图形问题
分析:利用直角三角形斜边上的中线等于斜边的一半以及等腰三角形的性质和三角形中位线性质进而得出四边形AEFD是平行四边形,进而求出EF的长.
解答: 解:连接△DBC两腰中点的线段EF,AE,
解:连接△DBC两腰中点的线段EF,AE,
由题意可得出:AD∥BC,
∵EF是△DBC的中位线,
∴EF
BC
∴AD∥BC,
∵BD=CD,
∴∠DBC=∠DCB,
则∠DEF=∠DFE,
∵AD∥EF,
∴∠ADE=∠DEF,
∵BE=DE,∠BAD=90°,
∴AE=DE=BE,
∴∠EAD=∠ADE,
∴∠AED=∠FDE,
∴AE∥DF,
∴四边形AEFD是平行四边形,
∴AD=EF=5.
故答案为:5.
 解:连接△DBC两腰中点的线段EF,AE,
解:连接△DBC两腰中点的线段EF,AE,由题意可得出:AD∥BC,
∵EF是△DBC的中位线,
∴EF
| ∥ |
. |
| 1 |
| 2 |
∴AD∥BC,
∵BD=CD,
∴∠DBC=∠DCB,
则∠DEF=∠DFE,
∵AD∥EF,
∴∠ADE=∠DEF,
∵BE=DE,∠BAD=90°,
∴AE=DE=BE,
∴∠EAD=∠ADE,
∴∠AED=∠FDE,
∴AE∥DF,
∴四边形AEFD是平行四边形,
∴AD=EF=5.
故答案为:5.
点评:此题主要考查了直角梯形以及等腰三角形和三角形中位线定理等知识,得出四边形AEFD是平行四边形是解题关键.

练习册系列答案
相关题目
计算
的值是( )
| (3-π)2 |
| A、3-π |
| B、-0.14 |
| C、π-3 |
| D、(3-π)2 |
数学表达式①-5<7;②3y-6>0;③a=6;④2x-3y;⑤a≠2;⑥7y-6>y+2,其中是不等式的有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
 实数a在数轴上的位置如图,化简
实数a在数轴上的位置如图,化简 如图是小刚画的一张脸,他对妹妹说:如果我用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成
如图是小刚画的一张脸,他对妹妹说:如果我用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成 如图,正比例函数y1=k1x与反比例函数y2=
如图,正比例函数y1=k1x与反比例函数y2=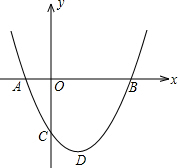 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中:
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中: