题目内容
10.当a2+a-1=0时,$\frac{2}{{a}^{2}+a}$-$\frac{a+2}{{a}^{2}+2a+1}$的结果是( )| A. | $\frac{-1-\sqrt{5}}{2}$ | B. | $\frac{-1+\sqrt{5}}{2}$ | C. | 1 | D. | 0 |
分析 先根据a2+a-1=0得出a2=1-a,再代入分式进行计算即可.
解答 解:∵a2+a-1=0,
∴a2=1-a,
∴原式=$\frac{2}{1-a+a}$-$\frac{a+2}{1-a+2a+1}$
=2-1
=1.
故选C.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.若分式$\frac{3}{x-2}$有意义,则x应满足的条件是( )
| A. | x≠0 | B. | x≥2 | C. | x≠2 | D. | x≤2 |
1.若x>y,则下列式子错误的是( )
| A. | x-3>y-3 | B. | -x>-y | C. | x+3>y+2 | D. | $\frac{x}{3}$>$\frac{y}{3}$ |
18. 如图所示,∠BAC和∠ACD是( )
如图所示,∠BAC和∠ACD是( )
 如图所示,∠BAC和∠ACD是( )
如图所示,∠BAC和∠ACD是( )| A. | 同位角 | B. | 同旁内角 | C. | 内错角 | D. | 以上结论都不对 |
5.下列判断不正确的是( )
| A. | 四个角相等的四边形是矩形 | B. | 对角线垂直的四边形是菱形 | ||
| C. | 对角线相等的平行四边形是矩形 | D. | 对角线垂直的平行四边形是菱形 |
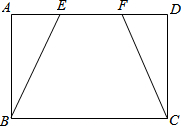 如图,矩形ABCD中,AD=3cm,AB=2cm,点E沿A→D方向移动,点F沿D→A方向移动,速度都是1cm/s.如果E、F两点同时分别从A、D出发移动,且当E、F两点相遇即停止.设移动时间为t(s)
如图,矩形ABCD中,AD=3cm,AB=2cm,点E沿A→D方向移动,点F沿D→A方向移动,速度都是1cm/s.如果E、F两点同时分别从A、D出发移动,且当E、F两点相遇即停止.设移动时间为t(s)