题目内容
20．
已知函数y=ax2+bx+c的图象如图示，画出下列函数图象．（1）y=ax2+bx+c+1；
（2）y=-ax2-bx-c；
（3）y=ax2-bx-c．
分析 根据图象上的点确定解析式然后根据：各题的要求确定解析式，然后利用描点法画二次函数图象．
解答 解：由图象可知抛物线的顶点为（1，-1），
∴y=a（x-1）2-1，
∵抛物线过（0，0）和（2，0），
∴0=a-1，
∴a=1，
∴函数为y=x2-2x；
（1）∵y=ax2+bx+c+1，
∴y=x2-2x+1=（x-1）2，
函数的图象为：
（2）∵y=-ax2-bx-c=-x2+2x=-（x-1）2+1，
函数的图象为：
（3）y=ax2-bx-c=x2+2x=（x+1）2-1，
函数的图象为：
点评 本题考查了二次函数的图象，五点法作图是常用的方法，要熟练掌握并灵活运用．
练习册系列答案
相关题目
如图，A、B是反比例函数y=$\frac{k}{x}$（k＞0）上两点，AC⊥x轴，BD⊥y轴，则S△ADE与S△BCE的关系如何？
已知正方形的两顶点在x轴上，另两个顶点在抛物线y=3-x2上，求这个正方形的面积．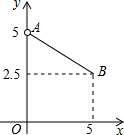
如图是函数y=$\frac{1}{2}$x+5的一部分图象，利用图象回答下列问题：