Question

11．如图，A、B是反比例函数y=$\frac{k}{x}$（k＞0）上两点，AC⊥x轴，BD⊥y轴，则S_△ADE与S_△BCE的关系如何？

Answer 1

分析 先过点A作AF⊥y轴于F，过点B作BG⊥x轴于G，根据反比例函数系数k的几何意义，可得矩形ACOF的面积=矩形BDOG的面积，进而得出△ADE的面积=△BCE的面积．

解答 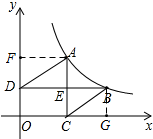解：过点A作AF⊥y轴于F，过点B作BG⊥x轴于G，
∵A、B是反比例函数y=$\frac{k}{x}$（k＞0）上两点，
∴矩形ACOF的面积=矩形BDOG的面积=k，
∴矩形AFDE的面积=矩形BECG的面积，
∵△ADE的面积=矩形AFDE的面积的一半，△BCE的面积=矩形BECG的面积的一半，
∴△ADE的面积=△BCE的面积，
故S_△ADE=S_△BCE．

点评 本题主要考查了反比例函数系数k的几何意义，在反比例函数y=$\frac{k}{x}$图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．解决问题的关键是作辅助线构造矩形．