题目内容
已知|a+3|与(b+1)2互为相反数,a、b分别对应数轴上的点A、B.
(1)求a、b的值.
(2)数轴上原点右侧存在点C,设甲、乙、丙三个动点分别从A、B、C三点同时运动,甲、乙向数轴正方向运动,丙向数轴负方向运动,甲、乙、丙运动速度分别为1、
、2(单位长度每秒),若它们在数轴上某处相遇,请求出C点对应的数是多少?
(3)运用(2)中所求C点对应的数,若甲、乙、丙出发地及速度大小均不变,同时向数轴负方向运动,问丙先追上谁?为什么?
(1)求a、b的值.
(2)数轴上原点右侧存在点C,设甲、乙、丙三个动点分别从A、B、C三点同时运动,甲、乙向数轴正方向运动,丙向数轴负方向运动,甲、乙、丙运动速度分别为1、
| 1 |
| 4 |
(3)运用(2)中所求C点对应的数,若甲、乙、丙出发地及速度大小均不变,同时向数轴负方向运动,问丙先追上谁?为什么?
考点:一元一次方程的应用,数轴
专题:应用题
分析:(1)利用非负数的性质求出a与b的值即可;
(2)设点C对应的数是x,根据题意列出方程,求出方程的解即可得到结果;
(3)设丙追上乙所需时间为a秒,丙追上甲所需时间为b秒,分别求出各自的时间,比较即可得到结果.
(2)设点C对应的数是x,根据题意列出方程,求出方程的解即可得到结果;
(3)设丙追上乙所需时间为a秒,丙追上甲所需时间为b秒,分别求出各自的时间,比较即可得到结果.
解答:解(1)∵|a+3|与(b+1)2互为相反数,即|a+3|+(b+1)2=0,
∴
,
解得:
;
(2)设C点对应的数是x,
则甲、丙从出发到相遇所需时间为
,乙、丙从出发到相遇所需时间为
,
∴
=
,
∴x=5;
(3)设丙追上乙所需时间为a秒,丙追上甲所需时间为b秒,
根据题意得:(2-
)a=5+1,即a=
;
(2-1)b=5+3,即b=8,
∵
<8,
∴丙先追上乙.
∴
|
解得:
|
(2)设C点对应的数是x,
则甲、丙从出发到相遇所需时间为
| x+3 |
| 1+2 |
| x+1 | ||
|
∴
| x+3 |
| 1+2 |
| x+1 | ||
|
∴x=5;
(3)设丙追上乙所需时间为a秒,丙追上甲所需时间为b秒,
根据题意得:(2-
| 1 |
| 4 |
| 24 |
| 7 |
(2-1)b=5+3,即b=8,
∵
| 24 |
| 7 |
∴丙先追上乙.
点评:此题考查了一元一 次方程的应用,找出题中的等量关系是解本题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
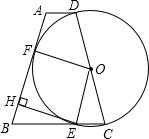 如同,在等腰梯形ABCD中,AD∥BC,O是CD边的中点,以O为圆心,OC长为半径作圆,交BC边于点E.过E作EH⊥AB,垂足为H,已知⊙O与AB边相切,切点为F,连结OF.
如同,在等腰梯形ABCD中,AD∥BC,O是CD边的中点,以O为圆心,OC长为半径作圆,交BC边于点E.过E作EH⊥AB,垂足为H,已知⊙O与AB边相切,切点为F,连结OF.