题目内容
阅读材料:如果x1、x2是一元二次方程ax2+bx+c=0(a≠0)的两根,那么,x1+x2=-
,x1•x2=
这就是著名的韦达定理.
现在我们利用韦达定理解决问题:
已知m与n是方程2x2-4x-3=0的两根,
(1)填空:m+n= ;m•n= ;
(2)计算
+
的值.
| b |
| a |
| c |
| a |
现在我们利用韦达定理解决问题:
已知m与n是方程2x2-4x-3=0的两根,
(1)填空:m+n=
(2)计算
| 1 |
| m |
| 1 |
| n |
考点:根与系数的关系
专题:计算题
分析:(1)根据根与系数的关系求解;
(2)把
+
进行通分,然后利用整体代入的方法计算.
(2)把
| 1 |
| m |
| 1 |
| n |
解答:解:(1)m+n=-
=2,mn=
=-
;
故答案为2,-
;
(2)原式=
=
=-
.
| -4 |
| 2 |
| -3 |
| 2 |
| 3 |
| 2 |
故答案为2,-
| 3 |
| 2 |
(2)原式=
| m+n |
| mn |
| 2 | ||
-
|
| 4 |
| 3 |
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-
,x1•x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
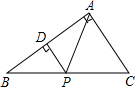 如图,在Rt△ABC中,∠BAC=90°,∠C=60°,BC=16,动点P在BC边上,过动点P作PD⊥AB,D为垂足.
如图,在Rt△ABC中,∠BAC=90°,∠C=60°,BC=16,动点P在BC边上,过动点P作PD⊥AB,D为垂足. 如图是某几何体的三视图.
如图是某几何体的三视图. 如图,∠1=47°,∠2=47°,∠D=47°,那么BC与DE平行吗?AB与CD呢?为什么?
如图,∠1=47°,∠2=47°,∠D=47°,那么BC与DE平行吗?AB与CD呢?为什么? 如图,已知∠AOD和∠BOC都是直角,∠DOC=62°,求∠AOB的度数.
如图,已知∠AOD和∠BOC都是直角,∠DOC=62°,求∠AOB的度数. 如图,一次函数y1=x+a的图象经过(-1,0)且与反比例函数
如图,一次函数y1=x+a的图象经过(-1,0)且与反比例函数