题目内容
4.直线y=x+1与直线y=2x-2的交点坐标是(3,4).分析 联立两直线的解析式即可求出交点的坐标.
解答 解:联立$\left\{\begin{array}{l}{y=x+1}\\{y=2x-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$
∴交点坐标为(3,4)
故答案为(3,4).
点评 本题考查两直线的交点坐标问题,解题的关键是联立两直线的解析式后解方程组,本题属于基础题型.

练习册系列答案
相关题目
14.已知a、b为实数,则a2+ab+b2-a-2b的最小值为( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
16.若反比例函数y=$\frac{k}{x}$(k≠0)经过(-2,3),则这个反比例函数一定经过( )
| A. | (-2,-3) | B. | (3,2) | C. | (3,-2) | D. | (-3,-2) |
13.一块砖的质量为m,体积为V,分成大小不等的两块,质量分别为m1,m2(m1>m2),体积分别为V1,V2,则( )
| A. | $\frac{m}{V}$=$\frac{{m}_{1}}{{V}_{1}}$=$\frac{{m}_{2}}{{V}_{2}}$ | B. | $\frac{m}{V}$>$\frac{{m}_{1}}{{V}_{1}}$>$\frac{{m}_{2}}{{V}_{2}}$ | ||
| C. | $\frac{{m}_{1}}{{V}_{1}}$=$\frac{{m}_{2}}{{V}_{2}}$≤$\frac{m}{V}$ | D. | $\frac{{m}_{2}}{{V}_{2}}$=$\frac{{m}_{1}}{{V}_{1}}$≥$\frac{m}{V}$ |
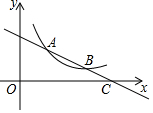 如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)在第一象限内交于A(x1,y1),B(x2,y2)两点,与x轴交于点C(x0,0)
如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)在第一象限内交于A(x1,y1),B(x2,y2)两点,与x轴交于点C(x0,0)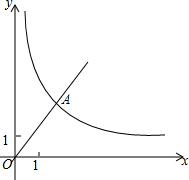 已知,如图,在平面直角坐标系xOy中,正比例函数y=$\frac{3}{2}$x的图象经过点A,点A的纵坐标为6,反比例函数y=$\frac{m}{x}$的图象也经过点A,第一象限内的点B在这个反比例函数的图象上,过点B作BC∥x轴,交y轴于点C,且AC=AB,求:
已知,如图,在平面直角坐标系xOy中,正比例函数y=$\frac{3}{2}$x的图象经过点A,点A的纵坐标为6,反比例函数y=$\frac{m}{x}$的图象也经过点A,第一象限内的点B在这个反比例函数的图象上,过点B作BC∥x轴,交y轴于点C,且AC=AB,求: