题目内容
8. 如图,在△ABC中,AB=AC.
如图,在△ABC中,AB=AC.(1)作△ABC的角平分线AD;(尺规作图,保留痕迹)
(2)在AD的延长线上任取一点E,连接BE、CE.
①求证:△BDE≌△CDE;
②当AE=2AD时,四边形ABEC是什么图形?请说明理由.
分析 (1)根据角平分线的作法,可得答案;
(2)①根据等腰三角形的“三线合一”可得BD=CD、∠BDE=∠CDE=90°,利用“SAS”即可判定△BDE≌△CDE;②根据菱形的判定:对角线互相平分且垂直的四边形是菱形,可得答案.
解答 解:(1)如图,线段AD即为所求;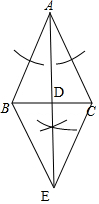
(2)①∵AB=AC,AD平分∠BAC,
∴BD=CD,AD⊥BC.
∴∠BDE=∠CDE=90°.
在△BDE和△CDE中,
∵$\left\{\begin{array}{l}{BD=CD}\\{∠BDE=∠CDE}\\{DE=DE}\end{array}\right.$
∴△BDE≌△CDE(SAS).
②∵AE=2AD,
∴AE=DE.
∵BD=CD,
∴四边形ABEC是平行四边形.
∵AD⊥BC,
∴平行四边形ABEC是菱形.
点评 本题考查了角平分线的尺规作图、等腰三角形的性质、全等三角形的判定与性质及菱形的判定,熟练掌握等腰三角形的“三线合一”及全等三角形和菱形的判定是解题的关键.

练习册系列答案
相关题目
18.直角三角形的一个锐角是另一个锐角的4倍,那么这个锐角的度数是( )
| A. | 18° | B. | 36° | C. | 54° | D. | 72° |
19.下列计算中,运算正确的是( )
| A. | (a-b)(a-b)=a2-b2 | B. | (x+2)(x-2)=x2-2 | ||
| C. | (2x+1)(2x-1)=2x2-1 | D. | (-3x+2)(-3x-2)=9x2-4 |
3.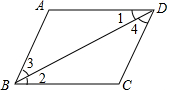 如图所示,下列判断中错误的是( )
如图所示,下列判断中错误的是( )
 如图所示,下列判断中错误的是( )
如图所示,下列判断中错误的是( )| A. | 因为AD∥BC,所以∠3=∠4 | B. | 因为AB∥CD,所以∠ABC+∠C=180° | ||
| C. | 因为∠1=∠2,所以AD∥BC | D. | 因为∠A+∠ADC=180°,所以AB∥CD |
17.某公司有A、B两种客车,它们的载客量和租金如下表,星星中学根据实际情况,计划用A、B型车共5辆,同时送七年级师生到校基地参加社会实践活动.
(1)若要保证租金费用不超过980元,请问该学校有哪几种租车方案?
(2)在(1)的条件下,若七年级师生共有150人,问哪种租车方案最省钱?
| A | B | |
| 载客量(人/辆) | 40 | 20 |
| 租金(元/辆) | 200 | 150 |
(2)在(1)的条件下,若七年级师生共有150人,问哪种租车方案最省钱?
