题目内容
7.先阅读理解下面的例题,再按要求解答下列问题:例题:解一元二次不等式x2-4>0
解:∵x2-4=﹙x+2﹚﹙x-2﹚,
∴x2-4>0可化为﹙x+2﹚﹙x-2﹚>0
由有理数乘法法则“两数相乘,同号得正”:得
①$\left\{\begin{array}{l}{x+2>0}\\{x-2>0}\end{array}\right.$ ②$\left\{\begin{array}{l}{x+2<0}\\{x-2<0}\end{array}\right.$
解不等式组①,得x>2,
解不等式组②,得x<-2,
∴﹙x+2﹚﹙x-2﹚>0的解集为x>2或x<-2,
即一元二次不等式x2-4>0的解集为x>2或x<-2.
(1)不等式$\frac{2x-1}{3x+6}$≥0的解集为x$≥\frac{1}{2}$或x<-2.
(2)解不等式:$\frac{2x+4}{3x-3}≤0$.
分析 (1)根据分式不等式≥0可以得到其分子、分母同号,从而转化为两个一元一次不等式组求解即可;
(2)根据分式不等式≤0可以得到其分子、分母异号,从而转化为两个一元一次不等式组求解即可.
解答 解:(1)∵$\frac{2x-1}{3x+6}$≥0,
可得:$\left\{\begin{array}{l}{2x-1≥0}\\{3x+6>0}\end{array}\right.$或$\left\{\begin{array}{l}{2x-1≤0}\\{3x+6<0}\end{array}\right.$,
解不等式组得:x$≥\frac{1}{2}$或x<-2;
故答案为:x$≥\frac{1}{2}$或x<-2
(2)∵$\frac{2x+4}{3x-3}≤0$,
可得:$\left\{\begin{array}{l}{2x+4≤0}\\{3x-3>0}\end{array}\right.$或$\left\{\begin{array}{l}{2x+4≥0}\\{3x-3<0}\end{array}\right.$,
解不等式组得:-2≤x<1.
点评 此题考查了不等式组的解法,利用了转化的思想,这种转化思想的依据为:两数相乘(除),同号得正,异号得负的取符号法则.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.大于-2.5而小于3.5的非负整数共有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
16.2014年北京市专利申请总件数是138111件,把138111写成科学记数法为( )
| A. | 13.8111×104 | B. | 1.38111×106 | C. | 13.8111×105 | D. | 1.38111×105 |
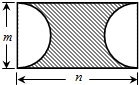 如图所示,阴影部分的面积为mn-$\frac{π{m}^{2}}{4}$(不化简也算对).
如图所示,阴影部分的面积为mn-$\frac{π{m}^{2}}{4}$(不化简也算对).