题目内容
4.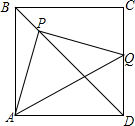 如图,正方形ABCD中,P为BD上一动点,过点P 作PQ⊥AP交CD边于点Q.
如图,正方形ABCD中,P为BD上一动点,过点P 作PQ⊥AP交CD边于点Q.(1)求证:PA=PQ;
(2)用等式表示PB2、PD2、AQ2之间的数量关系,并证明;
(3)点P从点B出发,沿BD方向移动,若移动的路径长为2,则AQ的中点M移动的路径长为$\sqrt{2}$(直接写出答案).
分析 (1)过点P作PE⊥AD于点E,PF⊥CD于点F,由正方形的性质得出PE=PF,证出四边形PEDF是正方形,得出∠EPF=90°,由ASA证明△APE≌△QPF,得出对应边相等即可;
(2)延长FP交AB于点G,由正方形的性质得出△PBG是等腰直角三角形,得出BP2=2PG2,同理PD2=2PE2,再由△PAQ是等腰直角三角形,得出AQ2=2PA2,即可得出结论;
(3)当点P在B点处时,点Q与点C重合,AQ的中点即为点O,则AQ的中点M移动的路径长为OM的长;连接PC,由正方形的性质得出PA=PC,再求出CQ的长,由三角形中位线定理求出OM的长即可.
解答 (1)证明:过点P作PE⊥AD于点E,PF⊥CD于点F,如图1所示:
∴∠PED=∠PEA=∠PFQ=90°,
∵四边形ABCD是正方形,
∴∠ADC=90°,∠ADB=∠CDB=45°,
∴PE=PF,
∴四边形PEDF是正方形,
∴∠EPF=90°,
∴∠EPQ+∠FPQ=90°,
∵AP⊥PQ,
∴∠EPQ+∠APE=90°,
∴∠APE=∠FPQ,
在△APE和△QPF中,$\left\{\begin{array}{l}{∠PEA=∠PFQ}&{\;}\\{PE=PF}&{\;}\\{∠APE=∠FPQ}&{\;}\end{array}\right.$,
∴△APE≌△QPF(ASA),
∴PA=PQ;
(2)解:PD2+PB2=AQ2,理由如下:
延长FP交AB于点G,如图2所示:
∵四边形ABCD是正方形,
∴AB∥CD,∠PBG=45°,
∴∠BGP=∠PFD=90°,
∴△PBG是等腰直角三角形,
由勾股定理得:BP2=2PG2,
同理:PD2=2PE2,
由(1)得PA=PQ,AP⊥PQ,
∴△PAQ是等腰直角三角形,
由勾股定理得:AQ2=2PA2,
∵∠AEP=∠AGP=∠BAD=90°,
∴四边形AEPG为矩形,
∴PE=AG,
∵PA2=AG2+PG2,
∴PD2+PB2=2PE2+2PG2=2AG2+2PG2=2AP2=AQ2;
(3)解:当点P在B点处时,点Q与点C重合,AQ的中点即为点O,
则AQ的中点M移动的路径长为OM的长;
连接PC,如图3所示: 由正方形的对称性得:PA=PC,
由正方形的对称性得:PA=PC,
由(2)得:△PBG是等腰直角三角形,
∴FC=BG=$\frac{BP}{\sqrt{2}}$=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,
由(1)得:PA=PQ,
∴PC=PQ,
∵PF⊥CQ,
∴FQ=FC=$\sqrt{2}$,
∴CQ=2$\sqrt{2}$,
∵O是AC的中点,M是AQ的中点,
∴OM=$\frac{1}{2}$CQ=$\sqrt{2}$;
故答案为:$\sqrt{2}$.
点评 本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、三角函数、勾股定理、三角形的中位线定理等知识;本题综合性强,难度较大.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案| A. | -4 | B. | 0 | C. | π | D. | -$\sqrt{3}$ |
| A. | x≠-1 | B. | x≠0 | C. | x≠1 | D. | x>1 |
| A. | 640×104 | B. | 64×105 | C. | 6.4×106 | D. | 0.64×107 |
| A. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| B. | 对角线相等的平行四边形是菱形 | |
| C. | 四条边都相等的四边形是正方形 | |
| D. | 顺次连接任意四边形的各边中点,得到的四边形是平行四边形 |
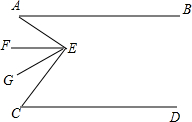 如图,已知AB∥CD,∠BAE=30°,∠DCE=60°,EF、EG三等分∠AEC(即∠AEF=∠FEG=∠GEC).
如图,已知AB∥CD,∠BAE=30°,∠DCE=60°,EF、EG三等分∠AEC(即∠AEF=∠FEG=∠GEC).