题目内容
16.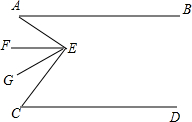 如图,已知AB∥CD,∠BAE=30°,∠DCE=60°,EF、EG三等分∠AEC(即∠AEF=∠FEG=∠GEC).
如图,已知AB∥CD,∠BAE=30°,∠DCE=60°,EF、EG三等分∠AEC(即∠AEF=∠FEG=∠GEC).(1)求∠AEF的度数;
(2)EF∥AB吗?为什么?
分析 (1)过E点做EF′∥AB,由平行线的性质得到F′E∥CD,求出∠AEC的度数,根据EF、EG三等分∠AEC求出∠AEF的度数;
(2)根据平行线的判定定理证明结论.
解答 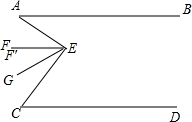 解:(1)过E点做EF′∥AB,则∠BAE=∠F′EA=30°,
解:(1)过E点做EF′∥AB,则∠BAE=∠F′EA=30°,
∵AB∥CD,
∴F′E∥CD,
∴∠DCE=∠F′EC=60°,
又∵∠AEC=∠F′EA+∠F′EC
∴∠AEC=90°,
∵EF、EG三等分∠AEC,
∴∠FEA=∠FEG=∠GEC,
∴∠FEG=30°;
(2)由(1)可知∠AEF=30°,
即∠AEF=∠BAE,
∴EF∥AB.
点评 本题考查的是平行线的性质和判定定理的综合运用,性质:两直线平行,同位角相等、内错角相等、同旁内角互补,判定:同位角相等、内错角相等、同旁内角互补,两直线平行.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
11.某中学随机地调查了50名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:
则这50名学生这一周在校的平均体育锻炼时间是6.4小时.
| 时间(小时) | 5 | 6 | 7 | 8 |
| 人数 | 10 | 15 | 20 | 5 |
1.如果四边形的四边中点所组成四边形是正方形,则下列说法正确的是( )
| A. | 原四边形的对角线相等 | B. | 原四边形的对角线互相垂直 | ||
| C. | 原四边形的对角线垂直平分 | D. | 原四边形的对角线互相垂直且相等 |
5.在Rt△ABC中,∠C=90°,AB=3,AC=2,则cosA的值是( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{5}}{3}$ |
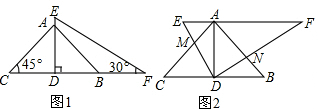
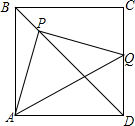 如图,正方形ABCD中,P为BD上一动点,过点P 作PQ⊥AP交CD边于点Q.
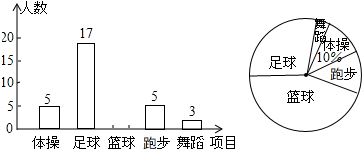
如图,正方形ABCD中,P为BD上一动点,过点P 作PQ⊥AP交CD边于点Q.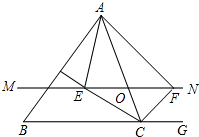 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.