题目内容
12.在Rt△ABC中,∠C=90°,a=1,b=2,则cosA=$\frac{2\sqrt{5}}{5}$.分析 首先求得c的长度,然后由余弦函数的定义求解即可.
解答 解:在Rt△ABC中,由勾股定理得:c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$.
cosA=$\frac{b}{c}$=$\frac{2\sqrt{5}}{5}$.
故答案为:$\frac{2\sqrt{5}}{5}$.
点评 本题主要考查的是勾股定理和锐角三角函数的定义,掌握余弦函数的定义是解题的关键.

练习册系列答案
相关题目
2.当x=2与x=-2时,代数式x4-2x2+3的两个值( )
| A. | 相等 | B. | 互为倒数 |
1.如果四边形的四边中点所组成四边形是正方形,则下列说法正确的是( )
| A. | 原四边形的对角线相等 | B. | 原四边形的对角线互相垂直 | ||
| C. | 原四边形的对角线垂直平分 | D. | 原四边形的对角线互相垂直且相等 |
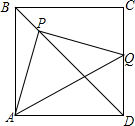 如图,正方形ABCD中,P为BD上一动点,过点P 作PQ⊥AP交CD边于点Q.
如图,正方形ABCD中,P为BD上一动点,过点P 作PQ⊥AP交CD边于点Q.