一个圆锥形的漏斗.小李用三角板测得其高度的尺寸如图所示.那么漏斗的斜壁AB的长度为( )A．4cmB．5cmC．5πcmD．$\sqrt{34}$cm 题目和参考答案——青夏教育精英家教网—

题目内容

12．

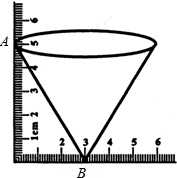一个圆锥形的漏斗，小李用三角板测得其高度的尺寸如图所示，那么漏斗的斜壁AB的长度为（　　）

A．

4cm

B．

5cm

C．

5πcm

D．

$\sqrt{34}$cm

分析根据题意及图形知本题是已知圆锥的底面半径及圆锥的高求圆锥的母线长，利用勾股定理即可求得．

解答解：根据题意知：圆锥的底面半径为3cm，高为5cm，
故圆锥的母线长AB=$\sqrt{{5}^{2}+{3}^{2}}$=$\sqrt{34}$cm．
故选D．

点评本题考查了圆锥的计算，解题的关键是知道圆锥的底面半径、高及圆锥的母线构成直角三角形．

练习册系列答案

相关题目

x²+y+y²

3．

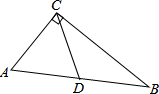如图，在Rt△ABC中，∠ACB=90°，D是AB的中点，若AB=16，则CD的长是（　　）

20．

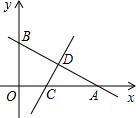如图，一次函数y=-$\frac{2}{3}$x+b的图象与x轴、y轴分别交于点A、B，线段AB的中点为D（3，2）．将△AOB沿直线CD折叠，使点A与点B重合，直线CD与x轴交于点C．
（1）求此一次函数的解析式；
（2）求点C的坐标；
（3）在坐标平面内存在点P（除点C外），使得以A、D、P为顶点的三角形与△ACD全等，请直接写出点P的坐标．

7．

如图，在边长为1个长度单位的小正方形组成的网格中，给出了△ABC（顶点是网格线的交点）．
（1）将△ABC向上平移5个单位得到△A₁B₁C₁，请画出△A₁B₁C₁；
（2）请以点A为位似中心画出△A₂B₂C₂，使△A₂B₂C₂与△ABC位似，且位似比为2：1．

17．（1）解不等式组$\left\{\begin{array}{l}{x+1＞0}\\{x≤\frac{x-2}{3}+2}\end{array}\right.$，并写出该不等式组的最大整数解．
（2）用因式分解法和公式法求解下列方程：9（x-5）²-24（x-5）+16=0．

4．已知，在Rt△ABC中，∠C=90°，AC=8，BC=6，D为AC的中点，E为斜边AB上一点，当AE=5或$\frac{7}{5}$时，BC=2DE．

1．

如图所示的运算程序中，若开始输入的x值为24，我们发现第1次输出的结果为 12，第2次输出的结果为6，…第2012次输出的结果为6．

2．

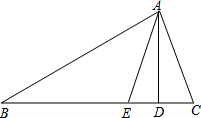如图，在△ABC中，AD是BC边上的高，AE是∠BAC的平分线，∠B=30°，∠DAE=20°，
（1）求∠C的度数．
（2）△ADC与△ADE全等吗？说明理由．

试题分类