题目内容
2.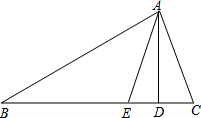 如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=30°,∠DAE=20°,
如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=30°,∠DAE=20°,(1)求∠C的度数.
(2)△ADC与△ADE全等吗?说明理由.
分析 (1)设∠DAC=x°,求出∠BAE=∠CAE=(x+20)°,∠BAC=2(x+20)°,∠C=(90-x)°,根据三角形内角和定理得出方程,求出方程的解即可;
(2)根据全等三角形的判定定理推出即可.
解答 解:(1)设∠DAC=x°,
∵AE是∠BAC的平分线,∠DAE=20°,
∴∠BAE=∠CAE=(x+20)°,∠BAC=2(x+20)°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠C=(90-x)°,
∵∠B+∠CAB+∠C=180°,
∴30°+2(x+20)°+(90-x)°=180°,
解得:x=20,
∴∠C=70°;
(2)△ADC与△ADE全等,
理由是:∠DAC=∠EAD=20°,
∵AD⊥BC,
∴∠ADC=∠ADE=90°,
在△ADC和△ADE中,
$\left\{\begin{array}{l}{∠DAC=∠EAD}\\{AD=AD}\\{∠ADC=∠ADE}\end{array}\right.$,
∴△ADC≌△ADE(ASA).
点评 本题考查了全等三角形的判定定理,三角形内角和定理,角平分线定义的应用,能根据题意得出方程和能运用全等三角形的判定定理进行推理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,难度适中.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
12.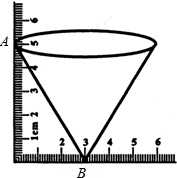 一个圆锥形的漏斗,小李用三角板测得其高度的尺寸如图所示,那么漏斗的斜壁AB的长度为( )
一个圆锥形的漏斗,小李用三角板测得其高度的尺寸如图所示,那么漏斗的斜壁AB的长度为( )
 一个圆锥形的漏斗,小李用三角板测得其高度的尺寸如图所示,那么漏斗的斜壁AB的长度为( )
一个圆锥形的漏斗,小李用三角板测得其高度的尺寸如图所示,那么漏斗的斜壁AB的长度为( )| A. | 4cm | B. | 5cm | C. | 5πcm | D. | $\sqrt{34}$cm |
14.下列多项式中,能用公式法分解因式的是( )
| A. | m2+n2 | B. | a2-ab+b2 | C. | -m2+n2 | D. | -a2-b2 |
11.下面调查中,适宜采用全面调查方式的是( )
| A. | 调查全国中小学生身体素质状况 | |
| B. | 调查重庆市冷饮市场某种品牌冰淇淋的质量情况 | |
| C. | 调查我校初2013级某班学生出生日期 | |
| D. | 调查我国居民对汽车废气污染环境的看法 |
12.据媒体预测报道说,2015年中国GDP总和将达到687380亿美元,将其中的687380亿美元化成科学记数法( )
| A. | 68738×108 | B. | 687380×108 | C. | 6.8738×1013 | D. | 6.8738×1012 |
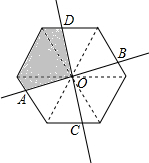 如图,正六边形中,点A在一边上运动,AO交六边形的另一边于B,过O作AB的垂线交六边形于C,D,形成如图所示的阴影部分.小姜设计了两个方案:①把如图所示的飞镖盘纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是$\frac{1}{4}$.②以O为旋转中心,把六边形做成转盘,则指针落在阴影部分的概率是$\frac{1}{4}$.那么以上两种方案正确的是( )
如图,正六边形中,点A在一边上运动,AO交六边形的另一边于B,过O作AB的垂线交六边形于C,D,形成如图所示的阴影部分.小姜设计了两个方案:①把如图所示的飞镖盘纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是$\frac{1}{4}$.②以O为旋转中心,把六边形做成转盘,则指针落在阴影部分的概率是$\frac{1}{4}$.那么以上两种方案正确的是( )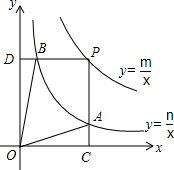 函数y=$\frac{m}{x}$和y=$\frac{n}{x}$在第一象限内的图象如图,点P是y=$\frac{m}{x}$的图象上一点,PC⊥x轴于点C,交y=$\frac{n}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{n}{x}$的图象于点B,且PA=3CA,tan∠DOB=$\frac{1}{5}$,SOAPB=3,则点B的坐标为($\frac{\sqrt{5}}{5}$,$\sqrt{5}$).
函数y=$\frac{m}{x}$和y=$\frac{n}{x}$在第一象限内的图象如图,点P是y=$\frac{m}{x}$的图象上一点,PC⊥x轴于点C,交y=$\frac{n}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{n}{x}$的图象于点B,且PA=3CA,tan∠DOB=$\frac{1}{5}$,SOAPB=3,则点B的坐标为($\frac{\sqrt{5}}{5}$,$\sqrt{5}$).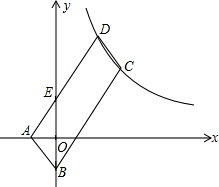 如图,平行四边形ABCD的顶点A,B的坐标分别是A(-2,0),B(0,-4),顶点C,D在双曲线y=$\frac{k}{x}$上,边AD交y轴于E点,且四边形BCDE的面积是△ABE面积的5倍,则k=48.
如图,平行四边形ABCD的顶点A,B的坐标分别是A(-2,0),B(0,-4),顶点C,D在双曲线y=$\frac{k}{x}$上,边AD交y轴于E点,且四边形BCDE的面积是△ABE面积的5倍,则k=48.