题目内容
17.(1)解不等式组$\left\{\begin{array}{l}{x+1>0}\\{x≤\frac{x-2}{3}+2}\end{array}\right.$,并写出该不等式组的最大整数解.(2)用因式分解法和公式法求解下列方程:9(x-5)2-24(x-5)+16=0.
分析 (1)先求出每个不等式的解集,再求出不等式组的解集即可;
(2)先因式分解,即可得出两个一元一次方程,求出方程的解即可;整理后求出b2-4ac的值,再代入公式求出即可.
解答 解:(1)$\left\{\begin{array}{l}{x+1>0①}\\{x≤\frac{x-2}{3}+2②}\end{array}\right.$
∵解不等式①得:x>-1,
解不等式②得:x≤2,
∴不等式组的解集为-1<x≤2,
∴不等式组的最大整数解是2;
(2)9(x-5)2-24(x-5)+16=0,
方法一:[3(x-5)-4][3(x-5)-4]=0,
开方得:3(x-5)-4=0,3(x-5)-4=0,
解得:x1=x2=$\frac{19}{3}$;
方法二:整理得:9x2-114x+361=0,
b2-4a=(-114)2-4×9×361=0,
x=$\frac{114±\sqrt{0}}{2×9}$,
x1=x2=$\frac{19}{3}$.
点评 本题考查了解一元一次不等式组,不等式组的整数解,解一元二次方程的应用,解(1)的此题的关键是能求出不等式组的解集,解(2)的关键是能正确运用各个方法解一元二次方程,此题属于中档题目,难度适中.

练习册系列答案
相关题目
7.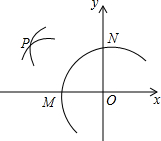 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(m,n-3),则m与n的数量关系为( )
如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(m,n-3),则m与n的数量关系为( )
 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(m,n-3),则m与n的数量关系为( )
如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(m,n-3),则m与n的数量关系为( )| A. | M-n=-3 | B. | m+n=-3 | C. | m-n=3 | D. | m+n=3 |
12.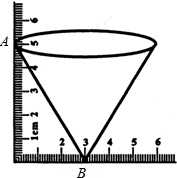 一个圆锥形的漏斗,小李用三角板测得其高度的尺寸如图所示,那么漏斗的斜壁AB的长度为( )
一个圆锥形的漏斗,小李用三角板测得其高度的尺寸如图所示,那么漏斗的斜壁AB的长度为( )
 一个圆锥形的漏斗,小李用三角板测得其高度的尺寸如图所示,那么漏斗的斜壁AB的长度为( )
一个圆锥形的漏斗,小李用三角板测得其高度的尺寸如图所示,那么漏斗的斜壁AB的长度为( )| A. | 4cm | B. | 5cm | C. | 5πcm | D. | $\sqrt{34}$cm |
 如图所示,把一块长方形纸片ABCD沿EF折叠,若∠EFB=58°,则∠BFN=64°.
如图所示,把一块长方形纸片ABCD沿EF折叠,若∠EFB=58°,则∠BFN=64°.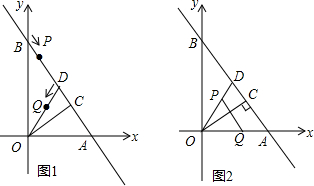
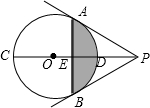 如图,CD为⊙O的直径,P是CD延长线上一点,PA为⊙O的切线,点A为切点,过A点作AB⊥PC,交PC于E,交⊙O于B,连结PB.
如图,CD为⊙O的直径,P是CD延长线上一点,PA为⊙O的切线,点A为切点,过A点作AB⊥PC,交PC于E,交⊙O于B,连结PB.