题目内容
15.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
①抛物线与x轴的一个交点为(3,0)
②函数y=ax2+bx+c的最大值为6.125
③抛物线的对称轴是直线x=$\frac{1}{2}$
④在对称轴左侧,y随x增大而增大.
分析 根据表中数据和抛物线的对称性:可知当x=0时,y=6,当x=1时,y=6,可得对称轴为x=$\frac{0+1}{2}$=$\frac{1}{2}$;(-2,0)与(3,0)对称,即抛物线与x轴的交点为(-2,0)和(3,0);抛物线的开口向下,求得函数y=-(x-$\frac{1}{2}$)2+$\frac{25}{4}$的最大值为6.125;在对称轴左侧,y随x增大而增大.
解答 解:∵当x=0时,y=6,当x=1时,y=6,
∴对称轴为x=$\frac{0+1}{2}$=$\frac{1}{2}$;
∴(-2,0)与(3,0)对称,
∴抛物线与x轴的一个交点为(3,0),
设抛物线解析式为y=a(x-$\frac{1}{2}$)2+k,代入(-2,0),0,6)求得函数y=-(x-$\frac{1}{2}$)2+$\frac{25}{4}$,
∵抛物线的开口向下,
∴函数的最大值为6.125;在对称轴左侧,y随x增大而增大;
正确的是①②③④.
故答案为:①②③④.
点评 本题考查了抛物线y=ax2+bx+c的性质:抛物线是轴对称图形,它与x轴的两个交点是对称点,对称轴与抛物线的交点为抛物线的顶点;a<0时,函数有最大值,在对称轴左侧,y随x增大而增大.

练习册系列答案
相关题目
3. 如图,在△ABC中,AB的中垂线交BC于点E,若BE=2,则A、E两点的距离是( )
如图,在△ABC中,AB的中垂线交BC于点E,若BE=2,则A、E两点的距离是( )
 如图,在△ABC中,AB的中垂线交BC于点E,若BE=2,则A、E两点的距离是( )
如图,在△ABC中,AB的中垂线交BC于点E,若BE=2,则A、E两点的距离是( )| A. | 4 | B. | 2 | C. | 3 | D. | $\frac{1}{2}$ |
20.若一元二次方程2x(kx-4)-x2+6=0无实数根,则k的最小整数值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |


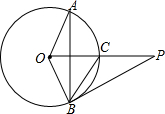 如图,已知P是⊙O外一点,PO交圆O于点C,OC=CP=2,弦AB⊥OC,∠AOB=120°,连接PB.
如图,已知P是⊙O外一点,PO交圆O于点C,OC=CP=2,弦AB⊥OC,∠AOB=120°,连接PB.