题目内容
10.在平面直角坐标系中,点O为坐标原点,点B在x轴正半轴上,且OB=2.(1)若点A在y轴正半轴上,∠OAB=30°且△ABO和△ABO′关于直线AB对称,求此时点O′的横坐标.
(2)已知,点M(m,0)、N(0,n)(2<n<4),将点B向上平移2个单位长度后得到点B′,若∠MB′N=90°,且mn=$\frac{15}{7}$,求m2+n2的值.
分析 (1)利用关于直线对称的性质得出△ABO≌△ABO′,进而得出∠O′CB=90°,即可得出∠BO′C=30°,则BC=$\frac{1}{2}$O′B=1,即可求出点O′的横坐标;
(2)首先得出△DB′N≌△BB′M(ASA),进而得出m2+n2=(m+n)2-2mn即可得出答案.
解答 解:(1)如图1: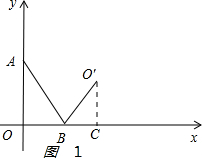
过点O′作O′C⊥x轴,垂足为点C,
∵△ABO和△ABO′关于直线AB对称,
∴△ABO≌△ABO′,
∴∠ABO=∠ABO′,OB=O′B=2,
∵∠OAB=30°,∠AOB=90°,
∴∠ABO=∠ABO′=60°,
∵∠OBO′+∠O′BC=180°,
∴∠O′BC=60°,
∵O′C⊥x轴,
∴∠O′CB=90°,
∴∠BO′C=30°,
∴BC=$\frac{1}{2}$O′B=1,
∴OC=OB+BC=3,
即点O′的横坐标为:3;
2)如图2: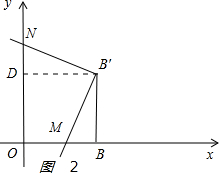
过点B′作B′D⊥y轴,垂足为点D,
∵点B在x轴正半轴上,且OB=2,
∴B(2,0),
∵点B向上平移2个单位长度后得到点B′,
∴B′(2,2),
∴BB′=B′D=2,
∵∠B′BM=90°,∠DOB=90°,∠B′DO=90°,
∴∠DB′B=90°,
∴∠DB′M+∠BB′M=90°,
∵∠MB′N=90°,
∴∠DB′M+∠DB′N=90°,
∴∠DB′N=∠BB′M,
在△DB′N和△BB′M中,
$\left\{\begin{array}{l}{∠DB′N=∠BB′M}\\{BB′=B′D}\\{∠B′DN=∠B′BM}\end{array}\right.$,
∴△DB′N≌△BB′M(ASA),
∴DN=BM,
∵点M(m,0),N(0,n),
∴BM=2-m,DN=n-2,
∴2-m=n-2,
即m+n=4,
∵mn=$\frac{15}{7}$,
∴m2+n2
=(m+n)2-2mn
=42-2×$\frac{15}{7}$
=16-$\frac{30}{7}$
=$\frac{82}{7}$.
点评 此题主要考查了全等三角形的判定与性质以及关于直线对称的性质等知识,熟练应用完全平方公式是解题关键

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
①抛物线与x轴的一个交点为(3,0)
②函数y=ax2+bx+c的最大值为6.125
③抛物线的对称轴是直线x=$\frac{1}{2}$
④在对称轴左侧,y随x增大而增大.
| A. | 1 | B. | 1或-1 | C. | -1 | D. | 2 |