题目内容
5.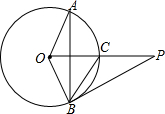 如图,已知P是⊙O外一点,PO交圆O于点C,OC=CP=2,弦AB⊥OC,∠AOB=120°,连接PB.
如图,已知P是⊙O外一点,PO交圆O于点C,OC=CP=2,弦AB⊥OC,∠AOB=120°,连接PB.(1)求BC的长;
(2)求证:PB是⊙O的切线.
分析 (1)由OA=OB,弦AB⊥OC,易证得△OBC是等边三角形,则可求得BC的长;
(2)由OC=CP=2,△OBC是等边三角形,可求得BC=CP,即可得∠P=∠CBP,又由等边三角形的性质,∠OBC=60°,∠CBP=30°,则可证得OB⊥BP,继而证得PB是⊙O的切线.
解答 (1)解:∵OA=OB,弦AB⊥OC,
∴∠AOC=∠BOC=$\frac{1}{2}$∠AOB=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴BC=OC=2;
(2)证明:∵OC=CP,BC=OC,
∴BC=CP,
∴∠CBP=∠CPB,
∵△OBC是等边三角形,
∴∠OBC=∠OCB=60°,
∴∠CBP=30°,
∴∠OBP=∠CBP+∠OBC=90°,
∴OB⊥BP,
∵点B在⊙O上,
∴PB是⊙O的切线.
点评 本题考查了切线的判定,等边三角形的判定与性质.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
15.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
从上表可知,下列说法中正确的是①②③④(填写序号)
①抛物线与x轴的一个交点为(3,0)
②函数y=ax2+bx+c的最大值为6.125
③抛物线的对称轴是直线x=$\frac{1}{2}$
④在对称轴左侧,y随x增大而增大.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
①抛物线与x轴的一个交点为(3,0)
②函数y=ax2+bx+c的最大值为6.125
③抛物线的对称轴是直线x=$\frac{1}{2}$
④在对称轴左侧,y随x增大而增大.
16.已知|a|=1,|b|=3,则|a+b|的值为( )
| A. | 2 | B. | 4 | C. | 2或4 | D. | ±2或±4. |
 已知:如图,正方形OABC的一个顶点为C(0,3).写出点O、B的坐标.
已知:如图,正方形OABC的一个顶点为C(0,3).写出点O、B的坐标.