题目内容
10. 完成下面推理过程:
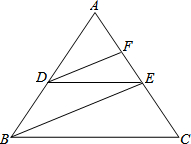
完成下面推理过程:如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:
∵DE∥BC(已知)
∴∠ADE=∠ABC.(两直线平行,同位角相等)
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF=$\frac{1}{2}$∠ADE,
∠ABE=$\frac{1}{2}$∠ABC.(角平分线定义)
∴∠ADF=∠ABE
∴DF∥BE.(同位角相等,两直线平行)
∴∠FDE=∠DEB.(两直线平行,内错角相等)
分析 根据平行线的性质得出∠ADE=∠ABC,根据角平分线定义得出∠ADF=$\frac{1}{2}$∠ADE,∠ABE=$\frac{1}{2}$∠ABC,推出∠ADF=∠ABE,根据平行线的判定得出DF∥BE即可.
解答 解:理由是:∵DE∥BC(已知),
∴∠ADE=∠ABC(两直线平行,同位角相等),
∵DF、BE分别平分ADE、∠ABC,
∴∠ADF=$\frac{1}{2}$∠ADE,
∠ABE=$\frac{1}{2}$∠ABC(角平分线定义),
∴∠ADF=∠ABE,
∴DF∥BE(同位角相等,两直线平行),
∴∠FDE=∠DEB(两直线平行,内错角相等),
故答案为:∠ABC,两直线平行,同位角相等,∠ADE,∠ABC,角平分线定义,BE,同位角相等,两直线平行,两直线平行,内错角相等.
点评 本题考查了平行线的性质和判定的应用,能熟记平行线的性质和判定定理是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.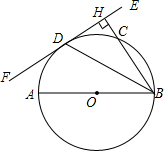 如图,AB为⊙O的直径,D是⊙O上一点,过D点作直线EF,BH⊥EF交⊙O于点C,垂足为H,且BD平分∠ABH.
如图,AB为⊙O的直径,D是⊙O上一点,过D点作直线EF,BH⊥EF交⊙O于点C,垂足为H,且BD平分∠ABH.
(1)求证:EF是⊙O的切线;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
 如图,AB为⊙O的直径,D是⊙O上一点,过D点作直线EF,BH⊥EF交⊙O于点C,垂足为H,且BD平分∠ABH.
如图,AB为⊙O的直径,D是⊙O上一点,过D点作直线EF,BH⊥EF交⊙O于点C,垂足为H,且BD平分∠ABH.(1)求证:EF是⊙O的切线;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
18.如果25x2-kxy+49y2是一个完全平方式,那么k的值是( )
| A. | 1225 | B. | 35 | C. | -70 | D. | ±70 |
15.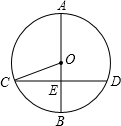 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么sin∠OCE=( )
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么sin∠OCE=( )
 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么sin∠OCE=( )
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么sin∠OCE=( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
2.用计算器计算时,其按键顺序为: ,则其运算结果为( )
,则其运算结果为( )
 ,则其运算结果为( )
,则其运算结果为( )| A. | -8 | B. | -6 | C. | 6 | D. | 8 |
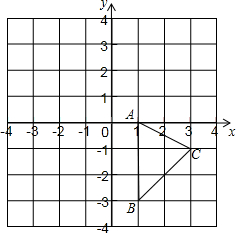 如图,平面直角坐标系中,△ABC的顶点都在网格点上,其中点A坐标为(1,0)
如图,平面直角坐标系中,△ABC的顶点都在网格点上,其中点A坐标为(1,0)