题目内容
19.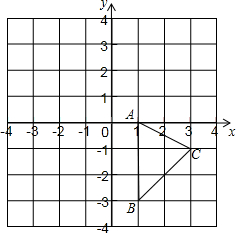 如图,平面直角坐标系中,△ABC的顶点都在网格点上,其中点A坐标为(1,0)
如图,平面直角坐标系中,△ABC的顶点都在网格点上,其中点A坐标为(1,0)(1)填空:点B的坐标为(1,-3),点C的坐标(3,-1);
(2)将△ABC先向左平移3个单位长度,再向上平移2个单位长度,得到△A1B1C1,画出△A1B1C1,并写出点A1的坐标;
(3)直接写出△A1B1C1的面积.
分析 (1)根据平面直角坐标系的特点写出点B、C的坐标;
(2)分别将点A、B、C先向左平移3个单位长度,再向上平移2个单位长度,得到三个点,然后顺次连接并写出点A1的坐标;
(3)根据三角形的面积公式求解即可.
解答  解:(1)B(1,-3),C(3,-1);
解:(1)B(1,-3),C(3,-1);
(2)所作图形如图所示:
点A1的坐标为(-2,2);
(3)S△A1B1C1=$\frac{1}{2}$×3×2=3.
故答案为:(1,-3),(3,-1).
点评 本题考查了根据平移变换作图,解答本题的关键是根据网格结构和直角坐标系的特点作出对应点的位置,然后顺次连接.

练习册系列答案
相关题目
14.下列各组数的大小比较错误的是( )
| A. | -$\frac{2}{3}$>-$\frac{3}{4}$ | B. | -$\frac{1}{3}$<-0.3 | C. | -(-2)>+(-3) | D. | -(-2.5)<|-2$\frac{1}{4}$| |
4.有理数,在数轴上的位置如图所示,下面结论正确的是( )


| A. | b-a<0 | B. | b-a>0 | C. | a-b<0 | D. | |a|>|b| |
 完成下面推理过程:
完成下面推理过程:
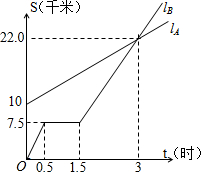 如图,lA lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
如图,lA lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.