题目内容
11.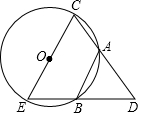 如图,CE是⊙O的直径,AB、AC是⊙O的两条弦,且AB=AC,延长CA、EB交于点D,问AD=AC吗?为什么?
如图,CE是⊙O的直径,AB、AC是⊙O的两条弦,且AB=AC,延长CA、EB交于点D,问AD=AC吗?为什么?
分析 先连接BC,构造直角三角形,根据AB=AC,得出∠ACB=∠ABC,再根据等角的余角相等,得出∠D=∠ABD,即可得出AB=AD,进而得到AD=AC.
解答  解:AD=AC.
解:AD=AC.
理由:连接BC,
∵CE是⊙O的直径,
∴∠CBE=90°,即∠CBD=90°,
∵AB=AC,
∴∠ACB=∠ABC,
又∵∠D+∠ACB=90°,∠ABD+∠ABC=90°,
∴∠D=∠ABD,
∴AB=AD,
∴AD=AC.
点评 本题主要考查了圆周角定理以及等腰三角形的判定与性质的运用,解决问题的关键是作辅助线构造直角三角形和等腰三角形.

练习册系列答案
相关题目
19.怎样测量某种食用油沸腾时的温度?因为油的沸点温度很高,用普通温度计很难直接测量,于是,小明设计了一个实验:取适量食用油在锅里用煤气灶开小火进行均匀加热,每隔5秒钟用普通温度计(测量范围在0℃-100℃之间)测量一次油温,结果如表:
而且小明发现50秒后该食用油沸腾.根据上述分析,你认为下面对该食用油沸点温度估计较为可靠的是( )
| 时间(s) | 0 | 5 | 10 | 15 |
| 食用油温度(℃) | 20 | 35 | 50 | 65 |
| A. | 85℃ | B. | 120℃ | C. | 150℃ | D. | 170℃ |
6.若|a|=$\frac{1}{5}$,|b|=5,则a÷b×$\frac{1}{b}$等于( )
| A. | $\frac{1}{125}$ | B. | ±$\frac{1}{125}$ | C. | ±$\frac{1}{5}$ | D. | -$\frac{1}{125}$或-$\frac{1}{5}$ |
3.平行四边形ABCD的四个顶点都在圆O上,那么四边形ABCD一定是( )
| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 以上都不对 |
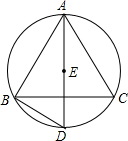 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D.
如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D. 如图,已知直线l及其两侧两点A、B.
如图,已知直线l及其两侧两点A、B. 如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),函数y=$\frac{k}{x}$(x<0)的图象过点P,则k的值为( )
如图,半径为5的⊙P与y轴交于点M(0,-4),N(0,-10),函数y=$\frac{k}{x}$(x<0)的图象过点P,则k的值为( )