题目内容
如图，AB是⊙O的直径，C，D是⊙O上两点，且AB=4cm，AC=CD=1cm，求BD的长．考点：垂径定理,勾股定理
专题：计算题
分析：连接OC，AD交AD于点E，根据AC=CD=1cm可知AD⊥BD，设OE=x，故可得出CE=OC-x，再根据勾股定理求出x的值，根据三角形中位线定理即可得出BD的长．
解答：
解：连接OC，AD，
∵AB是⊙O的直径，AB=4cm，
∴∠ADB=90°，OA=2cm，
∵AC=CD=1cm，
∴AD⊥BD，
设OE=x，则CE=OC-x=2-x，
在Rt△ACE中，AE2+CE2=AC2，即AE2=AC2-CE2①，
在Rt△AOE中，AE2+OE2=OA2，即AE2=OA2-OE2①，
∴AC2-CE2=OA2-OE2，即12-（2-x）2=22-x2，解得x=
cm，
∵∠ADB=∠AEO，点O是AB的中点，
∴OE是△ABD的中位线，
∴BD=2OE=
cm．
解：连接OC，AD，∵AB是⊙O的直径，AB=4cm，
∴∠ADB=90°，OA=2cm，
∵AC=CD=1cm，
∴AD⊥BD，
设OE=x，则CE=OC-x=2-x，
在Rt△ACE中，AE2+CE2=AC2，即AE2=AC2-CE2①，
在Rt△AOE中，AE2+OE2=OA2，即AE2=OA2-OE2①，
∴AC2-CE2=OA2-OE2，即12-（2-x）2=22-x2，解得x=
| 7 |
| 4 |
∵∠ADB=∠AEO，点O是AB的中点，
∴OE是△ABD的中位线，
∴BD=2OE=
| 7 |
| 2 |
点评：本题考查的是垂径定理、勾股定理及三角形中位线定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
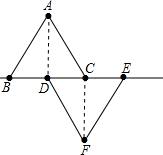在直角坐标中，有两个边长都为10cm的等边三角形△ABC和△DEF，且BC、DE与x轴重合，B与原点O重合，连结AD、CF．
如图，四边形ABCD为平行四边形，M、N分别从D到A、从B到C，速度相同，E、F分别从A到B、从C到D，速度相同．他们之间用绳子连紧．