题目内容
P是平行四边形ABCD的边CD上的一点，求证：S△ABP=
S?ABCD．
| 1 |
| 2 |
考点：平行四边形的性质
专题：
分析：如图，作辅助线，借助面积公式问题即可解决．
解答：
解：如图，过点P作PQ⊥AB于点Q；
则S△ABP=
AB•PQ，而平行四边形ABCD的面积=AB×PQ，
则S△ABP=
S?ABCD．
解：如图，过点P作PQ⊥AB于点Q；则S△ABP=
| 1 |
| 2 |
则S△ABP=
| 1 |
| 2 |
点评：该题考查了平行四边形的性质及其应用问题；解题的关键是灵活运用有关定理来分析、判断、推理或解答．
练习册系列答案
相关题目
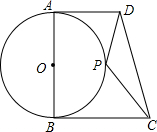已知：AB是⊙O的直径，AD、BC是⊙O的切线，P是⊙O上一动点，若AD=3，AB=4，BC=6，则△PCD的面积的最小值是（ ）
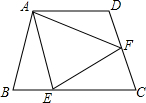如图，在四边形ABCD中，AB=AD，∠ABC+∠ADC=180°．E，F分别是BC，CD上的点，且∠EAF=