题目内容
用反证法证明:在同一圆中,如果两条弦不等,那么它们的弦心距也不等.
考点:反证法
专题:证明题
分析:首先从结论的反面出发进而假设结论不成立,即在同一个圆中,如果两条弦不等,弦心距可能相等,再利用勾股定理结合已知得出矛盾,进而得出答案.
解答: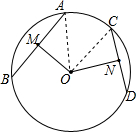 证明:假设结论不成立,即在同一个圆中,如果两条弦不等,弦心距可能相等,
证明:假设结论不成立,即在同一个圆中,如果两条弦不等,弦心距可能相等,
设圆心为O,弦AB≠弦CD,
设AB中点为M,CD中点为N,
则OM⊥AB,ON⊥CD,且OM=ON,
根据弦长性质,AM=
AB,CN=
CD,
由勾股定理可知:OA2=AM2+OM2=
AB2+OM2,
OC2=CN2+ON2=
CD2+ON2
∵OA=OC=半径,
∴
AB2+OM2=
CD2+ON2
又∵OM=ON,则
AB2=
CD2,
即AB=CD,与假设AB≠CD矛盾,假设不成立,
故在同一个圆中,如果两条弦不等,它们的弦心距不等.
 证明:假设结论不成立,即在同一个圆中,如果两条弦不等,弦心距可能相等,
证明:假设结论不成立,即在同一个圆中,如果两条弦不等,弦心距可能相等,设圆心为O,弦AB≠弦CD,
设AB中点为M,CD中点为N,
则OM⊥AB,ON⊥CD,且OM=ON,
根据弦长性质,AM=
| 1 |
| 2 |
| 1 |
| 2 |
由勾股定理可知:OA2=AM2+OM2=
| 1 |
| 4 |
OC2=CN2+ON2=
| 1 |
| 4 |
∵OA=OC=半径,
∴
| 1 |
| 4 |
| 1 |
| 4 |
又∵OM=ON,则
| 1 |
| 4 |
| 1 |
| 4 |
即AB=CD,与假设AB≠CD矛盾,假设不成立,
故在同一个圆中,如果两条弦不等,它们的弦心距不等.
点评:此题主要考查了反证法以及勾股定理,根据题意结合勾股定理求出是解题关键.

练习册系列答案
相关题目
甲乙两地相距20千米,某人从甲地去乙地,先步行走了8千米,又骑自行车到达乙地,共用了3小时,如果这个人骑自行车的速度是步行速度的3倍,那么他步行的速度是( )
| A、4千米/时 |
| B、6千米/时 |
| C、3千米/时 |
| D、8千米/时 |
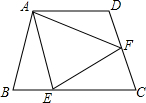 如图,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°.E,F分别是BC,CD上的点,且∠EAF=
如图,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°.E,F分别是BC,CD上的点,且∠EAF=
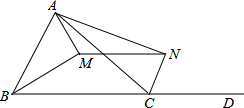 如图,BM平分∠ABC,AM⊥BM,CN平分∠ACD,AN⊥CN.请问:MN与AB、BC、AC之间的关系,并证明.
如图,BM平分∠ABC,AM⊥BM,CN平分∠ACD,AN⊥CN.请问:MN与AB、BC、AC之间的关系,并证明.