题目内容
19．直角三角形有两边长分别为5，9，则该直角三角形第三边为2$\sqrt{14}$或$\sqrt{106}$．分析 由于直角三角形的斜边不明确，故应分9为直角三角形的斜边与直角边两种情况进行讨论．
解答 解：当9为直角三角形的斜边时，该直角三角形第三边=$\sqrt{{9}^{2}-{5}^{2}}$=$\sqrt{81-25}$=2$\sqrt{14}$；
当9为直角三角形的直角边时，该直角三角形第三边=$\sqrt{{9}^{2}+{5}^{2}}$=$\sqrt{81+25}$=$\sqrt{106}$=$\sqrt{106}$．
故答案为：2$\sqrt{14}$或$\sqrt{106}$．
点评 本题考查的是勾股定理，在解答此题时要注意进行分类讨论，不要漏解．
练习册系列答案
相关题目
10．若最简二次根式$\sqrt{3a-8}$与$\sqrt{17-2a}$是同类二次根式，则a的取值为（ ）
| A． | a=4 | B． | a=5 | C． | a=6 | D． | a=7 |
4．
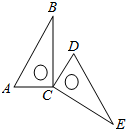如图一个含30°角的直角三角板ABC绕其直角顶点C旋转到△DCE的位置，当D、E、B三点在同一条直线上时，此时的旋转角∠BCE=（ ）
如图一个含30°角的直角三角板ABC绕其直角顶点C旋转到△DCE的位置，当D、E、B三点在同一条直线上时，此时的旋转角∠BCE=（ ）| A． | 105° | B． | 120° | C． | 135° | D． | 150° |
8．若⊙O1与⊙O2相切，且它们的半径分别是方程x2-6x+5=0的两根，则圆心距为（ ）
| A． | 1 | B． | 5 | C． | 4或6 | D． | 1或5 |
9．
在长方形OABC中，AB=3，BC=2，芳芳建立了如图所示的平面直角坐标系，则点B的坐标是（ ）
在长方形OABC中，AB=3，BC=2，芳芳建立了如图所示的平面直角坐标系，则点B的坐标是（ ）| A． | （3，2） | B． | （2，3） | C． | （-3，2） | D． | （-2，3） |