题目内容
4．
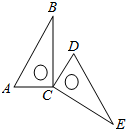如图一个含30°角的直角三角板ABC绕其直角顶点C旋转到△DCE的位置，当D、E、B三点在同一条直线上时，此时的旋转角∠BCE=（ ）| A． | 105° | B． | 120° | C． | 135° | D． | 150° |
分析 连接BD，则△BCE是等腰三角形，根据等腰三角形的性质求得∠CBE，则∠BCE即可求得．
解答 
解：连接BD．
∵BC=CE，
∴∠CBE=∠E=30°，
∴∠BCE=180°-30°-30°=120°．
故选B．
点评 本题考查了旋转的性质以及等腰三角形的性质，正确理解△BCE是等腰三角形是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
9．
如图，线段CD两个端点的坐标分别为C（3，3），D（4，1），以原点O为位似中心，在第一象限内将线段CD放大为原来的2倍后得到线段AB，则端点B的坐标为（ ）
如图，线段CD两个端点的坐标分别为C（3，3），D（4，1），以原点O为位似中心，在第一象限内将线段CD放大为原来的2倍后得到线段AB，则端点B的坐标为（ ）| A． | （6，6） | B． | （6，8） | C． | （8，6） | D． | （8，2） |
如图，在△ABC中，AB=AC=10cm，EF是边AB的垂直平分线，且△AEC的周长为24cm，则BC的长=14cm．