题目内容
9.若方程ax2+bx+c=0(a≠0)的两个根为x1,x2 ,且x1<x2 ,则x1=③(填写序号即可)①-$\frac{b}{2a}$-$\frac{\sqrt{{b}^{2}-4ac}}{2a}$;②-$\frac{b}{2a}$+$\frac{\sqrt{{b}^{2}-4ac}}{2a}$;
③-$\frac{b}{2a}$-$\frac{\sqrt{{b}^{2}-4ac}}{2|a|}$;④-$\frac{b}{2|a|}$-$\frac{\sqrt{{b}^{2}-4ac}}{2|a|}$.
分析 分两种情况:①若方程ax2+bx+c=0(a≠0)的一个根为x1=-$\frac{b}{2a}$+$\frac{\sqrt{{b}^{2}-4ac}}{2a}$时,②若方程ax2+bx+c=0(a≠0)的一个根为x1=-$\frac{b}{2a}$-$\frac{\sqrt{{b}^{2}-4ac}}{2a}$时,根据x1<x2 ,求得a的符号,讨论四个式子,与x1比较即可求得.
解答 解:若方程ax2+bx+c=0(a≠0)的一个根为x1=-$\frac{b}{2a}$+$\frac{\sqrt{{b}^{2}-4ac}}{2a}$时,
∵x1<x2 ,
∴-$\frac{b}{2a}$+$\frac{\sqrt{{b}^{2}-4ac}}{2a}$<-$\frac{b}{2a}$-$\frac{\sqrt{{b}^{2}-4ac}}{2a}$,
∴a<0,
∴-$\frac{b}{2a}$-$\frac{\sqrt{{b}^{2}-4ac}}{2|a|}$=-$\frac{b}{2a}$+$\frac{\sqrt{{b}^{2}-4ac}}{2a}$;
若方程ax2+bx+c=0(a≠0)的一个根为x1=-$\frac{b}{2a}$-$\frac{\sqrt{{b}^{2}-4ac}}{2a}$时,
∵x1<x2 ,
∴-$\frac{b}{2a}$-$\frac{\sqrt{{b}^{2}-4ac}}{2a}$<-$\frac{b}{2a}$+$\frac{\sqrt{{b}^{2}-4ac}}{2a}$,
∴a>0,
∴-$\frac{b}{2a}$-$\frac{\sqrt{{b}^{2}-4ac}}{2|a|}$=-$\frac{b}{2a}$-$\frac{\sqrt{{b}^{2}-4ac}}{2a}$;
故答案为③.
点评 此题考查了解一元二次方程-公式法,利用此方法解方程时首先将方程化为一般形式,找出二次项系数a,一次项系数b及常数项c,当b2-4ac≥0时,代入求根公式来求解.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 已知:如图,点A、E、F、C在同一直线上,∠A=∠C,AD=CB,AE=CF.
已知:如图,点A、E、F、C在同一直线上,∠A=∠C,AD=CB,AE=CF.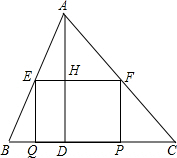 如图,在△ABC中,∠C=45°,BC=10,高AD=8,矩形EFPQ的一边QP在边上,E、F两点分别在AB、AC上,AD交EF于点H.
如图,在△ABC中,∠C=45°,BC=10,高AD=8,矩形EFPQ的一边QP在边上,E、F两点分别在AB、AC上,AD交EF于点H.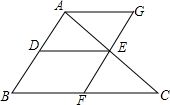 如图,DE是△ABC的中位线,过点E作AB的平行线交BC于点F,过点A作BC的平行线交直线EF于点G.线段DE,BF,FC之间有怎样的关系?请证明你的结论.
如图,DE是△ABC的中位线,过点E作AB的平行线交BC于点F,过点A作BC的平行线交直线EF于点G.线段DE,BF,FC之间有怎样的关系?请证明你的结论.