题目内容
1.已知:a=$\sqrt{2}$-1,b=2$\sqrt{2}$-$\sqrt{6}$,c=$\sqrt{6}$-2.试比较a、b、c的大小,并用“<”联结.
分析 先求出a,b,c的倒数,先比较倒数的大小,即可解答.
解答 解:$\frac{1}{a}=\frac{1}{\sqrt{2}-1}=\sqrt{2}+1$,
$\frac{1}{b}=\frac{1}{2\sqrt{2}-\sqrt{6}}=\frac{2\sqrt{2}+\sqrt{6}}{2}=\sqrt{2}+\sqrt{3}$,
$\frac{1}{c}=\frac{1}{\sqrt{6}-2}=\frac{\sqrt{6}+2}{2}=\sqrt{3}+1$,
∵$\sqrt{2}$+1$<\sqrt{3}$+1<$\sqrt{2}+\sqrt{3}$
∴$\frac{1}{a}<\frac{1}{c}<\frac{1}{b}$,
∴a>c>b.
点评 本题考查了实数比较大小,解决本题的关键是先进行比较倒数的大小.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知A(-2,4),B(6,2),AB交y轴于点C.
如图,已知A(-2,4),B(6,2),AB交y轴于点C.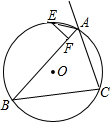 如图,△ABC内接于⊙O(AB>AC),E为$\widehat{BEC}$的中点,EF⊥AB于F,试说明:AB-AC=2AF.
如图,△ABC内接于⊙O(AB>AC),E为$\widehat{BEC}$的中点,EF⊥AB于F,试说明:AB-AC=2AF.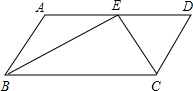 如图,在?ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12cm,CE=5cm.则?ABCD的周长为39,面积为60.
如图,在?ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12cm,CE=5cm.则?ABCD的周长为39,面积为60.