题目内容
19. 已知在△ABC中,AB=AC,∠D=∠BAC.
已知在△ABC中,AB=AC,∠D=∠BAC.(1)求证:DA=DC;
(2)求证:DC2-AC2=DB•DC.
分析 (1)根据等边对等角以及三角形的外角的性质证明∠DAC=∠C,即可证得;
(2)证明△DAC∽△ABC,利用相似三角形的对应边的比相等证得.
解答 证明:(1)∵AB=AC,
∴∠ABC=∠C,
又∵∠ABC=∠D+∠DAB,
又∵∠D=∠BAC,
∴∠D+∠DAB=∠BAC+∠DAB=∠DAC,
∴∠DAC=∠C,
∴DA=DC;
(2)∵∠DAC=∠C,∠C=ABC,
∴△DAC∽△ABC,
∴$\frac{DC}{AC}=\frac{AC}{BC}$,
∴AC2=DC•BC=DC(DC-DB),即AC2=DC2-DB•DC,
∴DC2-AC2=DB•DC.
点评 本题考查了等腰三角形的性质:等边对等角以及相似三角形的判定与性质,证明∠DAC=∠C是关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
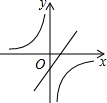
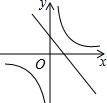
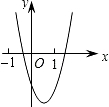 已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx-$\frac{b}{2a}$与反比例函数y=$\frac{ab}{x}$在同一坐标系内的大致图象是( )
已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx-$\frac{b}{2a}$与反比例函数y=$\frac{ab}{x}$在同一坐标系内的大致图象是( )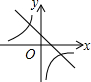

 如图,矩形ABCD中,对角线DB=2AB,若AD=3cm,则矩形ABCD的面积是多少cm2.
如图,矩形ABCD中,对角线DB=2AB,若AD=3cm,则矩形ABCD的面积是多少cm2.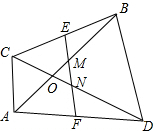 四边形ACBD中,AB、CD交于O,AB=CD,E、F是BC、AD的中点,判断△OMN的形状.
四边形ACBD中,AB、CD交于O,AB=CD,E、F是BC、AD的中点,判断△OMN的形状.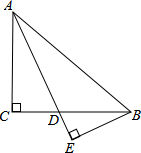 如图,在△ABC中,∠C=90°,AD是∠CAB的角平分线,BE⊥AE,垂足为点E.求证:△BDE∽△ABE.
如图,在△ABC中,∠C=90°,AD是∠CAB的角平分线,BE⊥AE,垂足为点E.求证:△BDE∽△ABE.