题目内容
4.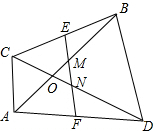 四边形ACBD中,AB、CD交于O,AB=CD,E、F是BC、AD的中点,判断△OMN的形状.
四边形ACBD中,AB、CD交于O,AB=CD,E、F是BC、AD的中点,判断△OMN的形状.
分析 △OMN为等腰三角形,理由为:取AC的中点P,连接PE,PF,如图所示,利用中位线定理得到PE与AB平行,且PE等于AB的一半,同时得到一对同位角相等;同理得到PF为中位线,得到PF与CD平行,且PF等于CD的一半,由AB=CD,得到PE=PF,利用等边对等边及等量代换得到∠OMN=∠ONM,利用等角对等边即可得证.
解答 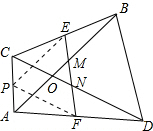 解:△OMN为等腰三角形,理由为:
解:△OMN为等腰三角形,理由为:
取AC的中点P,连接PE,PF,如图所示,
∵E为BC中点,即PE为△ABC中位线,
∴PE∥AB,且PE=$\frac{1}{2}$AB,
∴∠OMN=∠FEP,
同理PF为△ACD的中位线,
∴PF∥CD,且PF=$\frac{1}{2}$CD,
∴∠ONM=∠EFP,
∵AB=CD,
∴PE=PF,
∴∠EFP=∠FEP,
∴∠OMN=∠ONM,
则OM=ON,即△OMN为等腰三角形.
点评 此题考查了三角形中位线定理,以及等腰三角形的判定与性质,熟练掌握三角形中位线定理是解本题的关键.

练习册系列答案
相关题目
16.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与悬挂的物体的质量x(kg)间有下面的关系:
下列说法不正确的是( )
| 质量/kg | 0 | 1 | 2 | 3 | 4 | 5 |
| 长度/cm | 10 | 10.5 | 11 | 11.5 | 12 | 12.5 |
| A. | x和y都是变量,且x是自变量,y是因变量 | |
| B. | 弹簧不悬挂重物时的长度为0 | |
| C. | 在弹性限度内,物体质量每增加1kg,弹簧长度y增加0.5cm | |
| D. | 在弹性限度内,所挂物体的质量为7kg,弹簧长度为13.5cm |
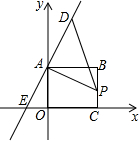 如图,已知四边形ABCD为矩形,O为坐标原点,点A的坐标为(0,6),点C的坐标为(8,0),点P是线段BC上一动点,已知点D是直线AE上位于第一象限的任意一点,直线AE与x轴交于点E(-3,0);
如图,已知四边形ABCD为矩形,O为坐标原点,点A的坐标为(0,6),点C的坐标为(8,0),点P是线段BC上一动点,已知点D是直线AE上位于第一象限的任意一点,直线AE与x轴交于点E(-3,0);
 已知在△ABC中,AB=AC,∠D=∠BAC.
已知在△ABC中,AB=AC,∠D=∠BAC.