题目内容
14．
如图，矩形ABCD中，对角线DB=2AB，若AD=3cm，则矩形ABCD的面积是多少cm2．
分析 设AB=x，则DB=2x，在直角△ABD中利用勾股定理即可列方程求得x的值，即AB的长，然后利用矩形的面积公式求解．
解答 解：设AB=x，则DB=2x，
∵矩形ABCD中，∠A=90°，
∴△ABD是直角三角形，
∴AB2+AD2=BD2，即x2+32=（2x）2，
解得：x=$\sqrt{3}$，
则AB=$\sqrt{3}$cm．
矩形ABCD的面积是：AB•AD=3$\sqrt{3}$（cm2）．
点评 本题考查了矩形的性质以及勾股定理，正确列方程求得AB的长是关键．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
如图，在⊙O中，AB、DE为直径，AB=24，点C在⊙O上，CO⊥AB，OA2+AC2=AD2，则∠ODB所对的弧长等于8π．
小刚用一张半径为12cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面（接缝忽略不计），如果做成的圆锥形小丑帽子的底面半径为5cm，那么这张扇形纸板的面积是60πcm2．
已知在△ABC中，AB=AC，∠D=∠BAC．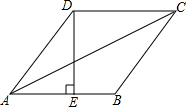
如图所示，在菱形ABCD中，E是AB的中点，且DE⊥AB，AB=2a．