题目内容
11.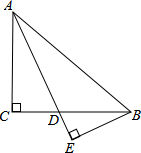 如图,在△ABC中,∠C=90°,AD是∠CAB的角平分线,BE⊥AE,垂足为点E.求证:△BDE∽△ABE.
如图,在△ABC中,∠C=90°,AD是∠CAB的角平分线,BE⊥AE,垂足为点E.求证:△BDE∽△ABE.
分析 根据角平分线的定义,可得∠CAD与∠DAB的关系,根据对顶角相等,可得∠ADC与∠BDE的关系,根据余角的性质,可得∠DAC与∠DBE的关系,根据有两个角相等的三角形相似,可得答案.
解答 证明:∵AD是∠CAB的角平分线,
∴∠CAD=∠DAB.
∵∠ADC与∠BDE是对顶角,
∴∠ADC=∠BDE.
∵BE⊥AE,垂足为点E,
∴∠E=90°=∠C.
∵∠CAD+∠ADC=∠DBE+∠BDE,
∴∠CAD=∠DBE,
∴∠DAB=∠DBE,
又∵∠E=∠E,
∴△BDE∽△ABE.
点评 本题考查了相似三角形的判定,利用了角平分线的定义,对顶角相等,余角的性质,相似三角形的判定,利用余角的性质得出∠CAD=∠DBE是解题关键.

练习册系列答案
相关题目
16.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与悬挂的物体的质量x(kg)间有下面的关系:
下列说法不正确的是( )
| 质量/kg | 0 | 1 | 2 | 3 | 4 | 5 |
| 长度/cm | 10 | 10.5 | 11 | 11.5 | 12 | 12.5 |
| A. | x和y都是变量,且x是自变量,y是因变量 | |
| B. | 弹簧不悬挂重物时的长度为0 | |
| C. | 在弹性限度内,物体质量每增加1kg,弹簧长度y增加0.5cm | |
| D. | 在弹性限度内,所挂物体的质量为7kg,弹簧长度为13.5cm |
 小刚用一张半径为12cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为5cm,那么这张扇形纸板的面积是60πcm2.
小刚用一张半径为12cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为5cm,那么这张扇形纸板的面积是60πcm2. 已知在△ABC中,AB=AC,∠D=∠BAC.
已知在△ABC中,AB=AC,∠D=∠BAC.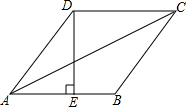 如图所示,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=2a.
如图所示,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=2a.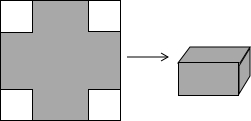 你能用正方形纸片制作长方体纸盒吗?如图,在正方形的四个角剪下同样大小的四个小正方形,把剩下的纸片折叠成一个无盖的纸盒,然后把剪下的四个小正方形纸片拼成一个大正方形作为纸盒的盖.如果我们希望做成的长方体的体积为4cm3,那么用作原料的大正方形纸片的边长应是多少.
你能用正方形纸片制作长方体纸盒吗?如图,在正方形的四个角剪下同样大小的四个小正方形,把剩下的纸片折叠成一个无盖的纸盒,然后把剪下的四个小正方形纸片拼成一个大正方形作为纸盒的盖.如果我们希望做成的长方体的体积为4cm3,那么用作原料的大正方形纸片的边长应是多少.