题目内容
7.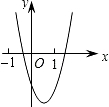 已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx-$\frac{b}{2a}$与反比例函数y=$\frac{ab}{x}$在同一坐标系内的大致图象是( )
已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx-$\frac{b}{2a}$与反比例函数y=$\frac{ab}{x}$在同一坐标系内的大致图象是( )| A. | 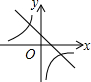 | B. | 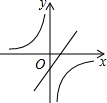 | C. |  | D. | 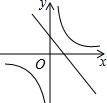 |
分析 根据二次函数图象与系数的关系,由抛物线对称轴的位置确定ab<0,由抛物线与y轴的交点位置确定c<0,然后根据一次函数图象与系数的关系可判断一次函数经过第一、二、四象限,根据反比例函数的性质得到反比例函数图象在第二、四象限,由此可对各选项进行判断.
解答 解:∵抛物线对称轴在y轴右侧,
∴ab<0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
对于一次函数y=cx-$\frac{b}{2a}$,c<0,图象经过第二、四象限;$\frac{b}{2a}$<0,图象与y轴的交点在x轴上方;
对于反比例函数y=$\frac{ab}{x}$,ab<0,图象分布在第二、四象限
故选:A.
点评 本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口,当a<0时,抛物线向下;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异);常数项c决定抛物线与y轴交点.也考查了一次函数图象与反比例函数图象.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
16.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与悬挂的物体的质量x(kg)间有下面的关系:
下列说法不正确的是( )
| 质量/kg | 0 | 1 | 2 | 3 | 4 | 5 |
| 长度/cm | 10 | 10.5 | 11 | 11.5 | 12 | 12.5 |
| A. | x和y都是变量,且x是自变量,y是因变量 | |
| B. | 弹簧不悬挂重物时的长度为0 | |
| C. | 在弹性限度内,物体质量每增加1kg,弹簧长度y增加0.5cm | |
| D. | 在弹性限度内,所挂物体的质量为7kg,弹簧长度为13.5cm |
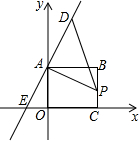 如图,已知四边形ABCD为矩形,O为坐标原点,点A的坐标为(0,6),点C的坐标为(8,0),点P是线段BC上一动点,已知点D是直线AE上位于第一象限的任意一点,直线AE与x轴交于点E(-3,0);
如图,已知四边形ABCD为矩形,O为坐标原点,点A的坐标为(0,6),点C的坐标为(8,0),点P是线段BC上一动点,已知点D是直线AE上位于第一象限的任意一点,直线AE与x轴交于点E(-3,0); 小刚用一张半径为12cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为5cm,那么这张扇形纸板的面积是60πcm2.
小刚用一张半径为12cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为5cm,那么这张扇形纸板的面积是60πcm2.
 已知在△ABC中,AB=AC,∠D=∠BAC.
已知在△ABC中,AB=AC,∠D=∠BAC.