题目内容
7.已知关于x,y的方程组$\left\{\begin{array}{l}{x-y=a+3}\\{2x+y=5a}\end{array}\right.$的解满足x+y>0,则a的取值范围是a>$\frac{1}{3}$.分析 把a看做已知数表示出方程组的解,代入已知不等式求出a的范围即可.
解答 解:$\left\{\begin{array}{l}{x-y=a+3①}\\{2x+y=5a②}\end{array}\right.$,
①+②得:3x=6a+3,即x=2a+1,
把x=2a+1代入①得:y=a-2,
代入x+y>0得:3a-1>0,
解得:a>$\frac{1}{3}$,
故答案为:a>$\frac{1}{3}$
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列式子中,正确的是( )
| A. | a2•a3=a6 | B. | (3ab2)3=9a3b6 | C. | (a2b)3÷(-ab)2=a4b | D. | (a-2)2=a2-4 |
19.函数y=$\sqrt{x+1}$中自变量x的取值范围是( )
| A. | x>0 | B. | x≥1 | C. | x>-1 | D. | x≥-1 |
17.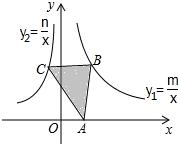 如图,已知△ABC,点A在x轴上,点B在双曲线y1=$\frac{m}{x}$(m>0,x>0)上.点C在双曲线y2=$\frac{n}{x}$(n<0,x<0)上.关于△ABC的面积.下列说法中正确的是( )
如图,已知△ABC,点A在x轴上,点B在双曲线y1=$\frac{m}{x}$(m>0,x>0)上.点C在双曲线y2=$\frac{n}{x}$(n<0,x<0)上.关于△ABC的面积.下列说法中正确的是( )
 如图,已知△ABC,点A在x轴上,点B在双曲线y1=$\frac{m}{x}$(m>0,x>0)上.点C在双曲线y2=$\frac{n}{x}$(n<0,x<0)上.关于△ABC的面积.下列说法中正确的是( )
如图,已知△ABC,点A在x轴上,点B在双曲线y1=$\frac{m}{x}$(m>0,x>0)上.点C在双曲线y2=$\frac{n}{x}$(n<0,x<0)上.关于△ABC的面积.下列说法中正确的是( )| A. | 当点A保持不动,点C,B随意移动时,△ABC的面积不变 | |
| B. | 当点A移动,BC保持不动时,△ABC的面积不变 | |
| C. | 不管点A,B,C怎么移动,△ABC的面积始终不变 | |
| D. | 不管点A,B,C怎么移动,只要BC与x轴平行,△ABC的面积就不变 |
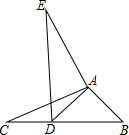 如图,在△ABC中,AB=2,BC=4,∠B=45°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为4-2$\sqrt{2}$.
如图,在△ABC中,AB=2,BC=4,∠B=45°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为4-2$\sqrt{2}$.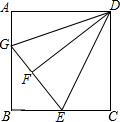 如图,正方形ABCD,AB=10,E为BC的中点,将正方形的边CD沿着DE折叠到DF,延长EF交AB于G,连接DG.
如图,正方形ABCD,AB=10,E为BC的中点,将正方形的边CD沿着DE折叠到DF,延长EF交AB于G,连接DG.