题目内容
18. 如图,点O是△ABC的两条角平分线的交点,过O作AO的垂线交AB于D,求证:△OBD∽△CBO.
如图,点O是△ABC的两条角平分线的交点,过O作AO的垂线交AB于D,求证:△OBD∽△CBO.
分析 由点O是△ABC的两条角平分线的交点,得到∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}∠$ACB,AO平分∠BAC,根据三角形的内角和得到∠ABC+∠ACB=180°-∠BAC,∠BAO=$\frac{1}{2}$∠BAC,于是得到∠BOC=180°-(∠1+∠2)=90°+$\frac{1}{2}$∠BAC=90°+∠BAO,根据AO⊥DO,得到∠AOD=90°,得到∠BDO=90°+∠BAO,求得∠BDO=∠BOC,于是得到结论.
解答 解:∵点O是△ABC的两条角平分线的交点,
∴∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}∠$ACB,AO平分∠BAC,
∵∠ABC+∠ACB=180°-∠BAC,∠BAO=$\frac{1}{2}$∠BAC,
∴∠1+∠2=90°-$\frac{1}{2}$∠BAC,
∴∠BOC=180°-(∠1+∠2)=90°+$\frac{1}{2}$∠BAC=90°+∠BAO,
∵∠BDO=∠AOD+∠BAO,
∵AO⊥DO,
∴∠AOD=90°,
∴∠BDO=90°+∠BAO,
∴∠BDO=∠BOC,
∵∠1=∠3,
∴△OBD∽△CBO.
点评 本题考查了相似三角形的判定和性质,三角形的内角和,三角形外角的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
8. 如图,已知点A在平面直角坐标系的位置,其坐标可能是( )
如图,已知点A在平面直角坐标系的位置,其坐标可能是( )
 如图,已知点A在平面直角坐标系的位置,其坐标可能是( )
如图,已知点A在平面直角坐标系的位置,其坐标可能是( )| A. | (3,4) | B. | (-3,4) | C. | (3,-4) | D. | (-3,-4) |
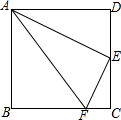 如图,在正方形ABCD中,E是CD的中点,FC=$\frac{1}{4}$BC,则图中有3对相似三角形,△ADE与△AEF的周长比为2:$\sqrt{5}$.
如图,在正方形ABCD中,E是CD的中点,FC=$\frac{1}{4}$BC,则图中有3对相似三角形,△ADE与△AEF的周长比为2:$\sqrt{5}$.