题目内容
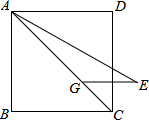如图，正方形ABCD中，点G为对角线AC上一点，AG=AB．∠CAE=15°且AE=AC，连接GE．将线段AE绕点A逆时针旋转得到线段AF，使DF=GE，则∠CAF的度数为考点：旋转的性质
专题：
分析：根据旋转的性质可得AE=AF，然后利用“边边边”证明△AGE和△ADF全等，根据全等三角形对应角相等可得∠DAF=∠CAE，然后分点F在AD的下方和上方两种情况讨论求解．
解答：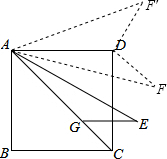
解：∵线段AE绕点A逆时针旋转得到线段AF，
∴AE=AF，
∵四边形ABCD是正方形，
∴AB=AD，
∵AG=AB，
∴AD=AG，
在△AGE和△ADF中，
，
∴△AGE≌△ADF（SSS），
∴∠DAF=∠CAE=15°，
∵AC为正方形ABCD的对角线，
∴∠CAD=45°，
点F在AD的下方时，∠CAF=∠CAD-∠DAF=45°-15°=30°，
点F在AD的上方时，∠CAF=∠CAD+∠DAF=45°+15°=60°，
综上所述，∠CAF的度数为30°或60°．
故答案为：30°或60°．
解：∵线段AE绕点A逆时针旋转得到线段AF，∴AE=AF，
∵四边形ABCD是正方形，
∴AB=AD，
∵AG=AB，
∴AD=AG，
在△AGE和△ADF中，
|
∴△AGE≌△ADF（SSS），
∴∠DAF=∠CAE=15°，
∵AC为正方形ABCD的对角线，
∴∠CAD=45°，
点F在AD的下方时，∠CAF=∠CAD-∠DAF=45°-15°=30°，
点F在AD的上方时，∠CAF=∠CAD+∠DAF=45°+15°=60°，
综上所述，∠CAF的度数为30°或60°．
故答案为：30°或60°．
点评：本题考查了旋转的性质，正方形的性质，全等三角形的判定与性质，熟记性质并求出∠DAF的度数是解题的关键，作出图形更形象直观．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
如图，排球运动员站在点O处练习发球，将球从点O正上方2米的点A处发出把球看成点，其运行的高度y（米）与运行的水平距离x（米）满足关系式y=a（x-6）2+h，已知球网与点O的水平距离为9米，高度为2.43米，球场的边界距点O的水平距离为18米．
如图是一个边长为1个单位的小正方形图案，将它平移或旋转或翻折后形成一个4×4的大正方形图案，画出你的一种设计图案．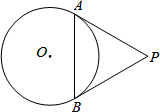
如图，PA，PB分别与⊙O相切于点A，B，连接AB．∠APB=60°，AB=5，则PA的长是
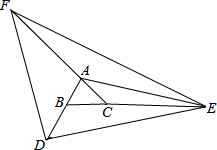如图，延长等边△ABC的边AB到D，使BD=3，延长BC到E，使CE=4，延长CA到F，使AF=5，若△DEF的面积为