题目内容
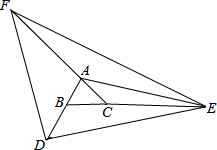如图，延长等边△ABC的边AB到D，使BD=3，延长BC到E，使CE=4，延长CA到F，使AF=5，若△DEF的面积为| 75 |
| 4 |
| 3 |
考点：等边三角形的性质,三角形的面积
专题：
分析：连接BF，CD，设△ABC的边长为x，面积为S，根据等边三角形的性质用x表示出S的值，再根据△ABC与△ACF等高可用S表示出△ACE的面积，同理可得出△AEF、△ABF、△BDF、△BDC、△CDE的面积，再根据△DEF的面积为
即可得出结论．
| 75 |
| 4 |
| 3 |
解答：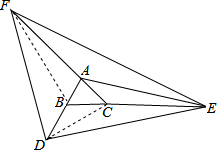
解：连接BF，CD．
设△ABC的边长为x，面积为S，
∵△ABC是等边三角形，
∴S=
x2．
∵△ABC与△ACE同高，CE=4，
∴S△ACE=
•S．
同理，△AEF与△ACE同高，
∴S△AEF=
•S△ACE=
•
•S，
∴S△ABF=
•S，S△BDF=
•S△ABF=
•
•S，S△BDC=
•S，S△CDE=
•S△BDC=
•
•S，
∴S△DEF=S△ABC+S△ACE+S△AEF+S△ABF+S△BDF+S△BDC+S△CDE=（1+
+
•
+
+
•
+
+
•
）S
=
S
=
•
x2=
，
解得x=2．
故△ABC的边长为2．
解：连接BF，CD．设△ABC的边长为x，面积为S，
∵△ABC是等边三角形，
∴S=
| ||
| 4 |
∵△ABC与△ACE同高，CE=4，
∴S△ACE=
| 4 |
| x |
同理，△AEF与△ACE同高，
∴S△AEF=
| 5 |
| x |
| 5 |
| x |
| 4 |
| x |
∴S△ABF=
| 5 |
| x |
| 3 |
| x |
| 3 |
| x |
| 5 |
| x |
| 3 |
| x |
| 4 |
| x |
| 4 |
| x |
| 3 |
| x |
∴S△DEF=S△ABC+S△ACE+S△AEF+S△ABF+S△BDF+S△BDC+S△CDE=（1+
| 4 |
| x |
| 5 |
| x |
| 4 |
| x |
| 5 |
| x |
| 3 |
| x |
| 5 |
| x |
| 3 |
| x |
| 4 |
| x |
| 3 |
| x |
=
| 12x+47+x2 |
| x2 |
=
| 12x+47+x2 |
| x2 |
| ||
| 4 |
| 75 |
| 4 |
| 3 |
解得x=2．
故△ABC的边长为2．
点评：本题考查的是等边三角形的性质，根据题意作出辅助线，构造出等高三角形是解答此题的关键．
练习册系列答案
快乐5加2金卷系列答案
相关题目
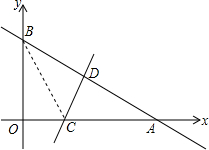如图，一次函数y=-
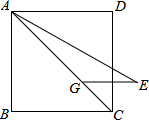如图，正方形ABCD中，点G为对角线AC上一点，AG=AB．∠CAE=15°且AE=AC，连接GE．将线段AE绕点A逆时针旋转得到线段AF，使DF=GE，则∠CAF的度数为
如图，AD是∠CAB内的一条射线，P为AD上一点，且∠APB、∠APC都是钝角，∠B=∠C，BP=CP．
画出如图几何体的主视图、左视图、俯视图．在-（-6），-（-6）2，-|-6|，（-6）2中，负数的个数为（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |