题目内容
将抛物线y=3x2+2先向右平移4个单位，再向下平移2个单位，所得抛物线的解析式为 ．
考点：二次函数图象与几何变换
专题：
分析：把抛物线平移的问题转化为点的平移：先确定抛物线y=3x2+2的顶点坐标，再求出顶点平移后的对应点的坐标，然后根据顶点式写出新抛物线解析式．
解答：解：抛物线y=3x2+2的顶点坐标为（0，2），把点（0，2）先向右平移4个单位，再向下平移2个单位得到点的坐标为（-4，0），所以平移后的抛物线的解析式为y=3（x-4）2．
故答案为y=3（x-4）2．
故答案为y=3（x-4）2．
点评：本题考查了二次函数与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．
练习册系列答案
相关题目
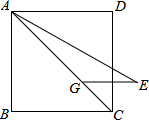如图，正方形ABCD中，点G为对角线AC上一点，AG=AB．∠CAE=15°且AE=AC，连接GE．将线段AE绕点A逆时针旋转得到线段AF，使DF=GE，则∠CAF的度数为
如图，AD是∠CAB内的一条射线，P为AD上一点，且∠APB、∠APC都是钝角，∠B=∠C，BP=CP．下列说法正确的是（ ）
A、单项式-
| ||||||
| B、0和a都是代数式 | ||||||
C、数a的
| ||||||
| D、合并同类项-n2-n2=0 |
画出如图几何体的主视图、左视图、俯视图．下列多项式乘法中，可以用平方差公式计算的是（ ）
| A、（x+y）（y+x） | ||||
| B、（2x-3y）（3x+2y） | ||||
| C、（-x-y）（x+y） | ||||
D、（-
|