题目内容
 如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x-6)2+h,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.
如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x-6)2+h,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.(1)当h=2.6时,求y与x的函数关系式.
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由.
考点:二次函数的应用
专题:
分析:(1)利用h=2.6,球从O点正上方2m的A处发出,将点(0,2)代入解析式求出即可;
(2)利用当x=9时,y=-
(x-6)2+2.6=2.45,当y=0时,-
(x-6)2+2.6=0,分别得出即可.
(2)利用当x=9时,y=-
| 1 |
| 60 |
| 1 |
| 60 |
解答:解:(1)∵h=2.6,球从O点正上方2m的A处发出,
∴抛物线y=a(x-6)2+h过点(0,2),
∴2=a(0-6)2+2.6,
解得:a=-
,
故y与x的关系式为:y=-
(x-6)2+2.6,
(2)当x=9时,y=-
(x-6)2+2.6=2.45>2.43,
所以球能过球网;
当y=0时,-
(x-6)2+2.6=0,
解得:x1=6+2
>18,x2=6-2
(舍去)
故会出界.
∴抛物线y=a(x-6)2+h过点(0,2),
∴2=a(0-6)2+2.6,
解得:a=-
| 1 |
| 60 |
故y与x的关系式为:y=-
| 1 |
| 60 |
(2)当x=9时,y=-
| 1 |
| 60 |
所以球能过球网;
当y=0时,-
| 1 |
| 60 |
解得:x1=6+2
| 39 |
| 39 |
故会出界.
点评:此题主要考查了二次函数的应用题,根据题意求出函数解析式是解题关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
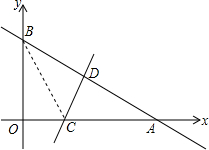 如图,一次函数y=-
如图,一次函数y=-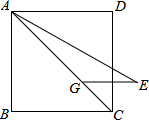 如图,正方形ABCD中,点G为对角线AC上一点,AG=AB.∠CAE=15°且AE=AC,连接GE.将线段AE绕点A逆时针旋转得到线段AF,使DF=GE,则∠CAF的度数为
如图,正方形ABCD中,点G为对角线AC上一点,AG=AB.∠CAE=15°且AE=AC,连接GE.将线段AE绕点A逆时针旋转得到线段AF,使DF=GE,则∠CAF的度数为 画出如图几何体的主视图、左视图、俯视图.
画出如图几何体的主视图、左视图、俯视图.