题目内容
1.如果一条直线l经过不同的三点A(a,b)、B(b,a)、C(a-b,b-a),那么直线l的函数解析式是y=-x.分析 设直线的解析式是y=kx+c,把A(a,b),B(b,a),C(a-b,b-a)代入得到方程组,求出方程组的解,根据一次函数的性质求出即可.
解答 解:设直线的解析式是y=kx+c,
把A(a,b),B(b,a),C(a-b,b-a)代入得:$\left\{\begin{array}{l}{b=ak+c}\\{a=bk+c}\\{b-a=(a-b)k+c}\end{array}\right.$,
解得:k=-1,c=0,
∴那么直线l的函数解析式是y=-x.
故答案为:y=-x.
点评 本题主要考查对解三元一次方程组,一次函数的性质,一次函数图象上点的坐标特征等知识点的理解和掌握,能熟练地运用性质进行说理是解此题的关键.

练习册系列答案
相关题目
13.已知$\frac{3}{x}$=$\frac{5}{y}$,则$\frac{{x}^{2}-xy+2{y}^{2}}{{x}^{2}-2xy}$的值为( )
| A. | -$\frac{44}{21}$ | B. | $\frac{8}{5}$ | C. | $\frac{44}{21}$ | D. | -$\frac{8}{5}$ |
 已知,如图,正八边形ABCDEFGH内按于半径为R的⊙O,求这个八边形的面积.
已知,如图,正八边形ABCDEFGH内按于半径为R的⊙O,求这个八边形的面积.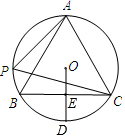 如图,A,P,B,C是⊙O上的四点,且满足∠BAC=∠APC=60°.
如图,A,P,B,C是⊙O上的四点,且满足∠BAC=∠APC=60°.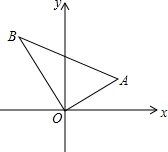 如图,Rt△ABO的顶点在原点,OA=12,AB=20,∠AOx=30°,求A,B两点的坐标,并求△AOB的面积.
如图,Rt△ABO的顶点在原点,OA=12,AB=20,∠AOx=30°,求A,B两点的坐标,并求△AOB的面积.