Question

16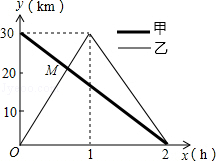．在一条笔直的公路上有A、B两地，甲骑自行车从A地到B地；乙骑自行车从B地到A地，到达A地后立即按原路返回，如图是甲、乙两人离B地的距离y（km）与行驶时间x（h）之间的函数图象，根据图象解答以下问题：
（1）写出A、B两地的距离；
（2）求出点M的坐标，并解释该点坐标所表示的实际意义．

Answer 1

分析 （1）根据函数图象就可以得出A、B两地的距离；
（2）根据速度=路程÷时间，结合函数图象求出甲、乙两人骑自行车的速度，再求出相遇时间，就可以求出乙离B地的距离，从而得出相遇点M的坐标．

解答 解：（1）由函数图象，得A、B两地的距离为30千米；

（2）由函数图象，得
甲的速度为：30÷2=15（千米/时），
乙的速度为：30÷1=30（千米/时），
则甲、乙两人相遇的时间为：30÷（15+30）=$\frac{2}{3}$（小时），
相遇时乙离开B地的距离为：$\frac{2}{3}$×30=20（千米），
所以点M的坐标为（$\frac{2}{3}$，20）．
该点坐标所表示的实际意义是：出发$\frac{2}{3}$小时时两车相遇，相遇点距离B地20千米．

点评 本题考查了一次函数的应用，相遇问题的数量关系的运用，解答时认真分析函数图象，弄清函数图象的意义是关键．