题目内容
11.化简求值:$\frac{{x}^{2}-8x+16}{{x}^{2}+2x}$÷($\frac{6}{x+2}$-1)+1,其中x选取-2,0,1,4中的一个合适的数.分析 可先把分式化简,再把x的值代入计算求值.
解答 解:原式=$\frac{(x-4)^{2}}{x(x+2)}$÷($\frac{6}{x+2}$-$\frac{x+2}{x+2}$)+1
=$\frac{(x-4)^{2}}{x(x+2)}$•$\frac{x+2}{4-x}$+1
=$\frac{4-x}{x}$+$\frac{x}{x}$
=$\frac{4}{x}$
当x=1时,原式=4.
点评 此题考查了分式的化简求值,难度不大,主要考查了因式分解和分式的混合计算;注意代入求值时保证所有分母不能为0.

练习册系列答案
相关题目
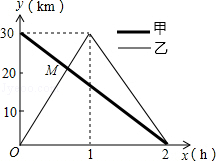 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题: