题目内容
9.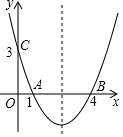 如图,抛物线y=ax2+bx+c经过A(1,0),B(4,0),C(0,3)三点,求抛物线的解析式.
如图,抛物线y=ax2+bx+c经过A(1,0),B(4,0),C(0,3)三点,求抛物线的解析式.
分析 由于已知抛物线与x轴的两交点坐标,则可设交点式y=a(x-1)(x-4),然后把C(0,3)代入求出a的值即可.
解答 解:设抛物线解析式为y=a(x-1)(x-4),
把C(0,3)代入得a•(-1)(-4)=3,解得a=$\frac{3}{4}$,
所以抛物线解析式为y=$\frac{3}{4}$(x-1)(x-4),即y=$\frac{3}{4}$x2-$\frac{15}{4}$x+3.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
1.表是二次函数y=ax2+bx+c的部分x,y的对应值:
(1)二次函数图象的开口向上,顶点坐标是(1,-2),m的值为2;
(2)当x>0时,y的取值范围是y≥-2;
(3)当抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时,n的取值范围是n>-3.
| x | … | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | m | $\frac{1}{4}$ | -1 | $-\frac{7}{4}$ | -2 | $-\frac{7}{4}$ | -1 | $\frac{1}{4}$ | 2 | … |
(2)当x>0时,y的取值范围是y≥-2;
(3)当抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时,n的取值范围是n>-3.

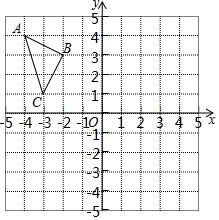 在如图的方格纸中,每个小正方形的边长都为l,△ABC的顶点坐标分别为A(-4,4)、B(-2,3)、C(-3,1).
在如图的方格纸中,每个小正方形的边长都为l,△ABC的顶点坐标分别为A(-4,4)、B(-2,3)、C(-3,1).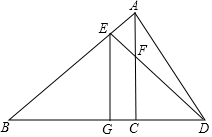 如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是AB上的一点,且在BD的垂直平分线EG上,DE交AC于点F,求证:点E在AF的垂直平分线上.
如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是AB上的一点,且在BD的垂直平分线EG上,DE交AC于点F,求证:点E在AF的垂直平分线上.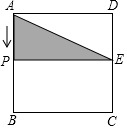 正方形ABCD的边长为4cm,点E是CD的中点,有一动点P由A出发沿B、C、D方向以2cm/秒的速度匀速运动,直至回到A点停止,设点P运动时间为t秒,当S△AEP=3cm2时,t的值为$\frac{3}{4}$或$\frac{17}{4}$或$\frac{23}{4}$或$\frac{13}{4}$.
正方形ABCD的边长为4cm,点E是CD的中点,有一动点P由A出发沿B、C、D方向以2cm/秒的速度匀速运动,直至回到A点停止,设点P运动时间为t秒,当S△AEP=3cm2时,t的值为$\frac{3}{4}$或$\frac{17}{4}$或$\frac{23}{4}$或$\frac{13}{4}$.