题目内容
13．有一根铁丝长为am，第一次用去一半少1m，第二次用去剩下的一半多1m，这条铁丝还剩余多少米？分析 第一次用去$\frac{1}{2}$a-1，第二次用去$\frac{1}{2}$[a-（$\frac{1}{2}$a-1）]+1，用a减去这两次的总量可得．
解答 解：根据题意，用去两次后还剩a-（$\frac{1}{2}$a-1）-$\frac{1}{2}$[a-（$\frac{1}{2}$a-1）]-1=$\frac{1}{4}$a-$\frac{1}{2}$，
答：这条铁丝还剩余（$\frac{1}{4}$a-$\frac{1}{2}$）米
点评 本题主要考查列代数式能力，根据题意表示出这两次用去的长度是关键．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
1．表是二次函数y=ax2+bx+c的部分x，y的对应值：
（1）二次函数图象的开口向上，顶点坐标是（1，-2），m的值为2；
（2）当x＞0时，y的取值范围是y≥-2；
（3）当抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时，n的取值范围是n＞-3．
| x | … | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | m | $\frac{1}{4}$ | -1 | $-\frac{7}{4}$ | -2 | $-\frac{7}{4}$ | -1 | $\frac{1}{4}$ | 2 | … |
（2）当x＞0时，y的取值范围是y≥-2；
（3）当抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时，n的取值范围是n＞-3．
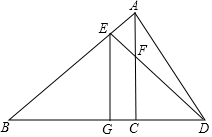如图，在△ABC中，∠ACB=90°，D是BC延长线上一点，E是AB上的一点，且在BD的垂直平分线EG上，DE交AC于点F，求证：点E在AF的垂直平分线上．
把边长为2厘米的6个相同正方体摆成如图的形式，