题目内容
11.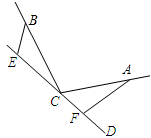 如图,∠BCA=α,CA=CB,C、E、F分别是直线CD上的三点,且∠BEC=∠CFA=α,请提出对EF,BE,AF三条线段之间数量关系的合理猜想,并证明.
如图,∠BCA=α,CA=CB,C、E、F分别是直线CD上的三点,且∠BEC=∠CFA=α,请提出对EF,BE,AF三条线段之间数量关系的合理猜想,并证明.
分析 由题意推出∠BCE=∠CAF,再由AAS定理证△BCE≌△CAF,继而得答案.
解答 EF=BE+AF.
证明:∵∠BEC=∠CFA=∠α,
∠α=∠BCA,
∠BCA+∠BCE+∠ACF=180°,
∠CFA+∠CAF+∠ACF=180°,
∴∠BCE=∠CAF,
在△BCE和△CAF中,
$\left\{\begin{array}{l}{∠BEC=∠CFA}\\{∠BCE=∠CAF}\\{CA=CB}\end{array}\right.$,
∴△BCE≌△CAF(AAS).
∴BE=CF,EC=FA,
∴EF=EC+CF=BE+AF.
点评 本题考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
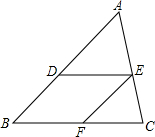 如图,点D,E,F分别在△ABC的边AB,AC,BC上,且DE∥BC,EF∥AB.求证:$\frac{AD}{AB}$=$\frac{BF}{BC}$.
如图,点D,E,F分别在△ABC的边AB,AC,BC上,且DE∥BC,EF∥AB.求证:$\frac{AD}{AB}$=$\frac{BF}{BC}$.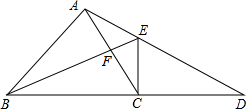 如图所示,在△ABC中,AB=AC,BC的延长线上有一点D,CD=BC,CE⊥BD于点C,交AD于点E,BE交AC于点F.
如图所示,在△ABC中,AB=AC,BC的延长线上有一点D,CD=BC,CE⊥BD于点C,交AD于点E,BE交AC于点F.