题目内容
9.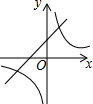 如图,一次函数y1=2x+2的图象与反比例函数y2=$\frac{k}{x}$(k为常数,且k≠0)图象都经过点A(m,3).
如图,一次函数y1=2x+2的图象与反比例函数y2=$\frac{k}{x}$(k为常数,且k≠0)图象都经过点A(m,3).①求点A的坐标及反比例函数的表达式;
②结合图象直接比较:当x<0时,y1与y2的大小.
分析 (1)把y=3代入y=2x+2可求得A的横坐标,则A的坐标即可确定,再利用待定系数法求得反比例函数的解析式;
(2)设一次函数y1=2x+2的图象与反比例函数y2=$\frac{3}{2x}$的图象在第三象限内交于点B,联立两函数解析式求出点B的坐标,再根据函数图象及图象的位置即可求解.
解答 解:(1)把y=3代入y=2x+2,得2x+2=3,
解得:x=$\frac{1}{2}$,
则A的坐标是($\frac{1}{2}$,3).
把($\frac{1}{2}$,3)代入y2=$\frac{k}{x}$得:k=1.5,
则反比例函数的解析式是:y2=$\frac{3}{2x}$;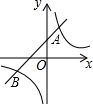 (2)设一次函数y1=2x+2的图象与反比例函数y2=$\frac{3}{2x}$的图象在第三象限内交于点B,
(2)设一次函数y1=2x+2的图象与反比例函数y2=$\frac{3}{2x}$的图象在第三象限内交于点B,
由2x+2=$\frac{3}{2x}$,解得x1=$\frac{1}{2}$,x2=-$\frac{3}{2}$,
当x=-$\frac{3}{2}$时,y=2×(-$\frac{3}{2}$)+2=-1,
则B(-$\frac{3}{2}$,-1).
根据图象得:-1.5<x<0时,y1>y2;
当x=-1.5时,y1=y2;
当x<-1.5时,y1<y2.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了待定系数法求反比例函数的解析式以及数形结合的思想.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
20.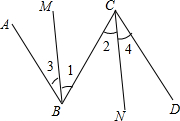 如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )
如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )
 如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )
如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )| A. | ∠1=∠2 | B. | ∠1=∠3且∠2=∠4 | ||
| C. | BM∥CN | D. | ∠1与∠2互补且不相等 |
18. 如图是某个几何体的三视图,则该几何体的形状是( )
如图是某个几何体的三视图,则该几何体的形状是( )
 如图是某个几何体的三视图,则该几何体的形状是( )
如图是某个几何体的三视图,则该几何体的形状是( )| A. | 长方体 | B. | 圆锥 | C. | 三棱锥 | D. | 直三棱柱 |
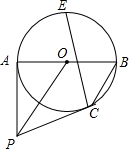 如图,AB是⊙O的直径,点P是⊙O外一点,PA切⊙O于点A,连接OP,过点B作BC∥OP交⊙O于点C,点E是$\widehat{AB}$的中点.
如图,AB是⊙O的直径,点P是⊙O外一点,PA切⊙O于点A,连接OP,过点B作BC∥OP交⊙O于点C,点E是$\widehat{AB}$的中点.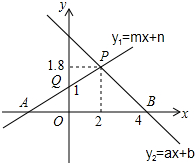 如图,根据图中信息解答下列问题:
如图,根据图中信息解答下列问题: 如图,点D在AC的垂直平分线上,AB∥CD,若∠ADC=130°,则∠BAC的度数是25°.
如图,点D在AC的垂直平分线上,AB∥CD,若∠ADC=130°,则∠BAC的度数是25°.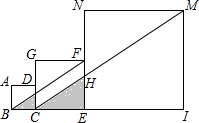 正方形ABCD的边长为1,正方形CEFG边长为2,正方形EIMN边长为4,以后的正方形边长按此规律扩大,其中点B、C、E、I…在同一条直线上,连接BF交CG于点K,连接CM交EN于点H,记△BCK的面积为S1,△CEH的面积为S2,…,依此规律,Sn=$\frac{{2}^{2n-2}}{3}$.
正方形ABCD的边长为1,正方形CEFG边长为2,正方形EIMN边长为4,以后的正方形边长按此规律扩大,其中点B、C、E、I…在同一条直线上,连接BF交CG于点K,连接CM交EN于点H,记△BCK的面积为S1,△CEH的面积为S2,…,依此规律,Sn=$\frac{{2}^{2n-2}}{3}$.