题目内容
6.计算:$\frac{\sqrt{5}}{\sqrt{3}+1}$+$\frac{\sqrt{3}}{\sqrt{5}-\sqrt{3}}$-$\frac{2+\sqrt{3}}{2-\sqrt{3}}$=$\sqrt{15}$+$\frac{\sqrt{5}}{2}$-$\frac{11}{2}$-4$\sqrt{3}$.分析 先分母有理化,然后合并即可.
解答 解:原式=$\frac{\sqrt{5}(\sqrt{3}+1)}{3-1}$+$\frac{\sqrt{3}(\sqrt{5}+\sqrt{3})}{5-3}$-$\frac{(2+\sqrt{3})^{2}}{4-3}$
=$\frac{\sqrt{15}+\sqrt{5}}{2}$+$\frac{\sqrt{15}+3}{2}$-7-4$\sqrt{3}$
=$\sqrt{15}$+$\frac{\sqrt{5}}{2}$-$\frac{11}{2}$-4$\sqrt{3}$.
故答案为$\sqrt{15}$+$\frac{\sqrt{5}}{2}$-$\frac{11}{2}$-4$\sqrt{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
4.若式子$\sqrt{x-5}$有意义,在实数范围内有意义,则x的取值范围是( )
| A. | x≥5 | B. | x≤5 | C. | x>5 | D. | x<5 |
5.当分式$\frac{x-1}{x+2}$的值为0时,x的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
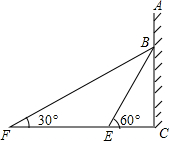 如图,在某建筑物AC上挂着宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为30°,再往条幅方向前行40米到达点E处,看到条幅顶端B,测得仰角为60°.
如图,在某建筑物AC上挂着宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为30°,再往条幅方向前行40米到达点E处,看到条幅顶端B,测得仰角为60°.