题目内容

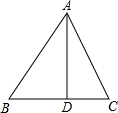如图，在△ABC中，AD⊥BC，sinB=
4
5
，BC=13，AD=12，则tanC的值
 
．
考点：解直角三角形
专题：
分析：先在Rt△ABD中利用三角函数求出AB，再根据勾股定理求出BD，进而可得出DC的值，即可求出tan∠C的值．
解答：解：∵AD⊥BC，AD=12，sinB=
4
5
，
∴
AD
AB
=
4
5
，
解得AB=15，
∴BD=
AB2-AD2
=
152-122
=9．
∵BC=13，
∴DC=BC-BD=4，
∴tanC=
AD
DC
=
12
4
=3．
故答案为：3．
点评：本题主要考查了解直角三角形，解题的关键是利用勾股定理求出BD的值．
练习册系列答案
相关题目
已知二次函数y=kx2-（k+3）x+3在x=0和x=4时的函数值相等．
（1）求该二次函数的表达式；
（2）画出该函数的图象，并结合图象直接写出当y＜0时，自变量x的取值范围；
（3）已知关于x的一元二次方程k2x2-
3
mx+m2-m=0，当-1≤m≤3时，判断此方程根的情况．
如果二次函数y=（m-1）x2+5x+m2-1的图象经过原点，那么m=
 
．
已知3x=2y，那么下列等式一定成立的是（　　）
A、x=2，y=3
B、
x
y
=
3
2
C、
x
y
=
2
3
D、3x+2y=0
某岛O为我国固有领土，对进入该岛12海里范围内的外国船只，我海监船将予以驱离．一天我一艘海监船巡航至岛O正南约14海里的A处，发现在其北偏东45°方向8
2
海里的B处有一艘可疑船入侵，立即向其发出警告信号．可以船在我海监船的警示下，开始掉头向正东方向行驶远离O岛，10分钟后，在A处的我海监船发现可疑船在北偏东53°方向的C处．
（1）请你通过计算，求出可疑船在B处时离岛O的距离
（2）求出可疑船驶离时的平均速度（参考数据sin53°≈0.8，cos53°≈0.6，tan53°≈
4
5
）
计算：3（
a
-
b
）-3
a
=
 
．
将抛物线y=2（x-1）2+1向上平移3个单位，那么平移后得到的抛物线的解析式是
 
．
如图，边长为2菱形ABCD中，∠DAB=60°，连接对角线AC，以AC为边作第二个菱形ACC1D1，使∠D1AC=60°；连接AC1，再以AC1为边作第三个菱形AC1C2D2，使∠D2AC1=60°；…，按此规律所作的第6个菱形的边长为
 
．
计算：
tan30°
cos245°
+
sin60°
sin30°
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网