题目内容
半径分别为8cm与6cm的⊙O1与⊙O2相交于A、B两点,圆心距O1O2的长为10cm,那么公共弦AB的长为 cm.
考点:相交两圆的性质
专题:
分析:根据相交两圆的性质以及垂径定理得出AC=
AB,进而利用勾股定理得出AC的长即可得出AB的长.
| 1 |
| 2 |
解答: 解:连接AO1,AO2.
解:连接AO1,AO2.
∵⊙O1,⊙O2相交于A、B两点,两圆半径分别为8cm和6cm,两圆的连心线O1O2的长为10cm,
∴O1O2⊥AB,
∴AC=
AB,
设O1C=x,则O2C=10-x,
∴82-x2=62-(10-x)2,
解得:x=6.4,
∴AC2=82-x2=64-4.82=23.04,
∴AC=4.8cm,
∴弦AB的长为:9.6cm.
故答案为:9.6.
 解:连接AO1,AO2.
解:连接AO1,AO2.∵⊙O1,⊙O2相交于A、B两点,两圆半径分别为8cm和6cm,两圆的连心线O1O2的长为10cm,
∴O1O2⊥AB,
∴AC=
| 1 |
| 2 |
设O1C=x,则O2C=10-x,
∴82-x2=62-(10-x)2,
解得:x=6.4,
∴AC2=82-x2=64-4.82=23.04,
∴AC=4.8cm,
∴弦AB的长为:9.6cm.
故答案为:9.6.
点评:此题考查了相交圆的性质与勾股定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想与方程思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
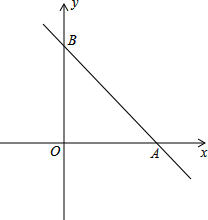 如图,在平面直角坐标系中,直线y=-
如图,在平面直角坐标系中,直线y=-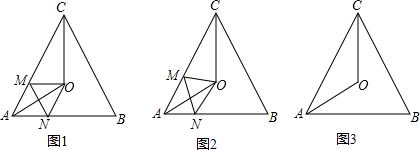
 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).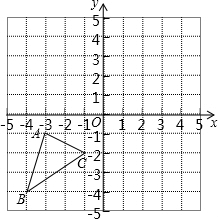 如图,在正方形网格中,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
如图,在正方形网格中,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题: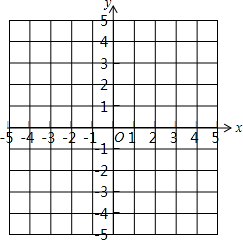 已知二次函数y=kx2-(k+3)x+3在x=0和x=4时的函数值相等.
已知二次函数y=kx2-(k+3)x+3在x=0和x=4时的函数值相等.